Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T00:03:41.885Z Has data issue: false hasContentIssue false
  • English
  • Français

Büchi’s Problem in Modular Arithmetic for Arbitrary Quadratic Polynomials

Part of: Sequences and sets

Published online by Cambridge University Press:  26 April 2019

Pablo Sáez ,
Xavier Vidaux  and
Maxim Vsemirnov
Pablo Sáez
Affiliation:
Concepción, Chile Email: [email protected]
Xavier Vidaux
Affiliation:
Universidad de Concepción, Facultad de Ciencias Físicas y Matemáticas, Departamento de Matemática, Casilla 160 C, Concepción, Chile Email: [email protected]
Maxim Vsemirnov
Affiliation:
St. Petersburg Department of V.A.Steklov Institute of Mathematics, 27 Fontanka, St. Petersburg, 191023, Russia St. Petersburg State University, Department of Mathematics and Mechanics, 28 University prospekt, St. Petersburg, 198504, Russia Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a prime 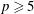$p\geqslant 5$ and an integer 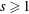$s\geqslant 1$, we show that there exists an integer 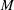$M$ such that for any quadratic polynomial 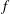$f$ with coefficients in the ring of integers modulo 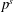$p^{s}$, such that 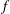$f$ is not a square, if a sequence 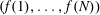$(f(1),\ldots ,f(N))$ is a sequence of squares, then 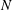$N$ is at most 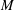$M$. We also provide some explicit formulas for the optimal 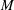$M$.

Keywords

Büchi sequenceHensley sequence

MSC classification

Primary: 11B50: Sequences (mod $m$)
Secondary: 11B83: Special sequences and polynomials
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 4 , December 2019 , pp. 876 - 885
Copyright
© Canadian Mathematical Society 2019 

Footnotes

All three authors were partially supported by the grants “Fondecyt research projects 1130134 and 1170315, Chile” to author X. V., from Conicyt. Author M. V. was partially supported by the government of the Russian Federation (grant 14.Z50.31.0030).

References

Allison, D., On square values of quadratics . Math. Proc. Cambridge Philos. Soc. 99(1986), no. 3, 381–383. https://doi.org/10.1017/S030500410006432X Google Scholar
An, T. T. H., Huang, H.-L., and Wang, J. T.-Z., Generalized Büchi’s problem for algebraic functions and meromorphic functions . Math. Z. 273(2013), no. 1–2, 95–122. https://doi.org/10.1007/s00209-012-0997-9 Google Scholar
An, T. T. H. and Wang, J. T. Y., Hensley’s problem for complex and non-Archimedean meromorphic functions . J. Math. Anal. Appl. 381(2011), no. 2, 661–677. https://doi.org/10.1016/j.jmaa.2011.03.025 Google Scholar
Bremner, A., On square values of quadratics . Acta Arith. 108(2003), 95–111. https://doi.org/10.4064/aa108-2-1 Google Scholar
Browkin, J. and Brzeziński, J., On sequences of squares with constant second differences . Canad. Math. Bull. 49‐4(2006), 481–491. https://doi.org/10.4153/CMB-2006-047-9 Google Scholar
Garcia-Fritz, N., Quadratic sequences of powers and Mohanty’s conjecture . Int. J. Number Theory 14(2018), no. 2, 479–507. https://doi.org/10.1142/S1793042118500306 Google Scholar
González-Jiménez, E. and Xarles, X., On symmetric square values of quadratic polynomials . Acta Arith. 149(2011), no. 2, 145–159. https://doi.org/10.4064/aa149-2-4 Google Scholar
Lipshitz, L., Quadratic forms, the five square problem, and diophantine equations , The collected works of J. Richard Büchi, eds. MacLane, S. and Siefkes, Dirk, Springer, 1990, pp. 677–680.Google Scholar
Mazur, B., Questions of decidability and undecidability in number theory . J. Symbolic Logic 59‐2(1994), 353–371. https://doi.org/10.2307/2275395 Google Scholar
Pasten, H., Büchi’s problem in any power for finite fields . Acta Arith. 149‐1(2011), 57–63. https://doi.org/10.4064/aa149-1-4 Google Scholar
Pasten, H., Pheidas, T., and Vidaux, X., A survey on Büchi’s problem: new presentations and open problems . Zapiski POMI 377(2010), 111–140. https://doi.org/10.1007/s10958-010-0181-x Google Scholar
Pasten, H. and Wang, J. T.-Y., Extensions of Büchi’s higher powers problem to positive characteristic . Int. Math. Res. Not. IMRN 2015 no. 11, 3263–3297.Google Scholar
Pheidas, T. and Vidaux, X., The analogue of Büchi’s problem for rational functions . J. London Math. Soc. 74(2006), no. 3, 545–565. https://doi.org/10.1112/S0024610706023283 Google Scholar
Pheidas, T. and Vidaux, X., Corrigendum: The analogue of Büchi’s problem for rational functions . J. London Math. Soc. 82(2010), 273–278. https://doi.org/10.1112/jlms/jdq002 Google Scholar
Sáez, P., Vidaux, X., and Vsemirnov, M., Optimal bounds for Büchi’s problem in modular arithmetic . J. Number Theory 149(2015), 368–403. https://doi.org/10.1016/j.jnt.2014.10.008 Google Scholar
Shlapentokh, A. and Vidaux, X., The analogue of Büchi’s problem for function fields . J. Algebra 330(2010), 482–506. https://doi.org/10.1016/j.jalgebra.2011.01.008 Google Scholar
Vojta, P., Diagonal quadratic forms and Hilbert’s Tenth Problem . In: Hilbert’s tenth problem: relations with arithmetic and algebraic geometry , Contemp. Math., 270, American Mathematical Society, Providence, RI, 2000, pp. 261–274. https://doi.org/10.1090/conm/270/04378 Google Scholar