Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T01:17:45.986Z Has data issue: false hasContentIssue false
  • English
  • Français

Bourgain Algebras of Spaces of n-Harmonic Functions in the Unit Polydisk

Published online by Cambridge University Press:  20 November 2018

Keiji Izuchi ,
Kazuhiro Kasuga  and
Yasuo Matsugu
Keiji Izuchi
Affiliation:
Department of Mathematics, Faculty of Science, Niigata University, Niigata 950-21, Japan
Kazuhiro Kasuga
Affiliation:
Department of Mathematics, Faculty of Science, Shinshu University, Matsumoto 390, Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let h∞(Dn) denote the space of all bounded n-harmonic functions on the unit polydisk Dn of Cn. In this paper we prove that the Bourgain algebra h∞(Dn)b and h∞(Dn)bb relative to the Lebesgue space L∞(Dn) are of the following forms:

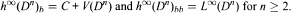
Here V(Dn) is the space of those functions 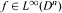such that 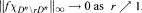, where 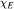denotes the characteristic function of a subset E of Dn.

Keywords

Primary: 32A35Secondary: 46J15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 39 , Issue 3 , 01 September 1996 , pp. 284 - 293
Copyright
Copyright © Canadian Mathematical Society 1996

References

1. Cima, J., Janson, S. and Yale, K., Completely continuous Hankel operators on H∞ and Bourgain algebras, Proc. Amer. Math. Soc. 105(1989), 121–125.Google Scholar
2. Cima, J., Stroethoff, K. and Yale, K., Bourgain algebras on the unit disk, Pacific J. Math. 160(1993), 27–41.Google Scholar
3. Cima, J. and Tiomoney, R., The Dunford-Pettis property for certain planar uniform algebras, Michigan Math. J. 34(1987), 99–104.Google Scholar
4. Ghatage, G., Sun, S. and Zheng, D., A remark on Bourgain algebras on the disk, Proc. Amer. Math. Soc. 114(1992), 395–398.Google Scholar
5. Gorkin, P. and Izuchi, K., Bourgain algebras on the maximal ideal space of H∞ , Rocky Mount. J., to appear.Google Scholar
6. Gorkin, P., Izuchi, K. and Mortini, R., Bourgain algebras of Douglas algebras, Canad. J. Math. 44(1992), 797–804.Google Scholar
7. Izuchi, K., Bourgain algebras of the disk, polydisk and ball algebras, Duke Math. J. 66(1992), 503—519.Google Scholar
8. Izuchi, K. and Matsugu, Y., Multipliers and Bourgain algebras of H∞ + C on the polydisk, Pacific J. Math. 171(1995), 167–208.Google Scholar
9. Izuchi, K., Stroethoff, K. and Yale, K., Bourgain algebras of spaces of harmonic functions, Michigan Math. J. 41(1994), 309–321.Google Scholar
10. Mortini, R. and Younis, R., Douglas algebras which are invariant under Bourgain map, Arch. Math. 59 (1992), 371–378.Google Scholar
11. Rudin, W., Function theoiy in poly discs, Benjamin, New York, 1969.Google Scholar
12. Rudin, W., Real and complex analysis, 3rd edition, McGraw-Hill, New York, 1987.Google Scholar
13. Sarason, D., Function theory on the unit circle, Virginia Polytechnic Institute and State University, Blacksburg, Va., 1978.Google Scholar