Published online by Cambridge University Press: 20 November 2018
A self-avoiding polygon is a lattice polygon consisting of a closed self-avoiding walk on a square lattice. Surprisingly little is known rigorously about the enumeration of self-avoiding polygons, although there are numerous conjectures that are believed to be true and strongly supported by numerical simulations. As an analogous problemto this study, we considermultiple self-avoiding polygons in a confined region as a model for multiple ring polymers in physics. We find rigorous lower and upper bounds for the number 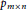 ${{p}_{m\times n}}$ of distinct multiple self-avoiding polygons in the
${{p}_{m\times n}}$ of distinct multiple self-avoiding polygons in the 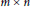 $m\,\times \,n$ rectangular grid on the square lattice. For
$m\,\times \,n$ rectangular grid on the square lattice. For  $m\,=\,2,\,{{p}_{2\times n}}\,=\,{{2}^{n-1}}\,-1$. And for integers
$m\,=\,2,\,{{p}_{2\times n}}\,=\,{{2}^{n-1}}\,-1$. And for integers 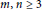 $m,\,n\,\ge \,3$,
$m,\,n\,\ge \,3$,
 $${{2}^{m+n-3}}\left( \frac{17}{10} \right){{\,}^{\left( m-2 \right)\left( n-2 \right)}}\,\le \,{{p}_{m\times n}}\,\le \,{{2}^{m+n-3}}\left( \frac{31}{16} \right){{\,}^{\left( m-2 \right)\left( n-2 \right)}}.$$
$${{2}^{m+n-3}}\left( \frac{17}{10} \right){{\,}^{\left( m-2 \right)\left( n-2 \right)}}\,\le \,{{p}_{m\times n}}\,\le \,{{2}^{m+n-3}}\left( \frac{31}{16} \right){{\,}^{\left( m-2 \right)\left( n-2 \right)}}.$$