Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-29T02:49:00.700Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundedness in a Quasi-Uniform Space

Published online by Cambridge University Press:  20 November 2018

M. G. Murdeshwar  and
K. K. Theckedath
M. G. Murdeshwar
Affiliation:
University of Alberta, Edmonton, Alberta
K. K. Theckedath
Affiliation:
Wilson College, Bombay 7wb, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Although a nontopological concept, boundedness seems to be of considerable importance in a topological space. 'There are many topological problems in which it is essential to be able to make this distinction' (between bounded and unbounded sets) [1]. Boundedness and in particular boundedness-preserving' uniform spaces appear to have applications to topological dynamics [4].

In spite of this importance, there have been only isolated attempts at developing the concept. Alexander [1] and Hu [7] tried the axiomatic approach. Hu, for example, calls a nonempty family 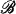of sets a boundedness if 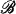is hereditary and closed under finite union.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 3 , September 1970 , pp. 367 - 370
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Alexander, J. W., On the concept of a topological space, Proc. Nat. Acad. Sci. U.S.A. 25 (1939), 52-54.Google Scholar
2. Bourbaki, N., Topologie générale, Hermann, Paris, 1950.Google Scholar
3. Bourbaki, N., Topologie générale, 4th éd., Hermann, Paris, 1965.Google Scholar
4. Bushaw, D., On boundedness in uniform spaces, Fund. Math. 56 (1965), 295-300.Google Scholar
5. Császár, A., Fondements de la topologie générale, Gauthier-Villars, Paris, 1960.Google Scholar
6. Hejcman, Jan, On Conservative uniform spaces, Comment. Math. Univ. Carolinae 7 (1966), 411-417.Google Scholar
7. Hu, S. T., Boundedness in a topological space, J. Math. Pures Appl. 28 (1949), 287-320.Google Scholar
8. Murdeshwar, M. G., and Naimpally, S. A., Quasi-uniform topological spaces, Noordhoff Groningen, 1966.Google Scholar