No CrossRef data available.
Article contents
A bound on the 
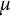$\mu $-invariants of supersingular elliptic curves
Published online by Cambridge University Press: 07 February 2025
Abstract
Let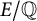 
$E/\mathbb {Q}$ be an elliptic curve and let p be a prime of good supersingular reduction. Attached to E are pairs of Iwasawa invariants 
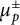$\mu _p^\pm $ and 
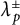$\lambda _p^\pm $ which encode arithmetic properties of E along the cyclotomic 
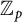$\mathbb {Z}_p$-extension of 
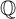$\mathbb {Q}$. A well-known conjecture of B. Perrin-Riou and R. Pollack asserts that 
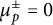$\mu _p^\pm =0$. We provide support for this conjecture by proving that for any 
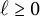$\ell \geq 0$, we have 
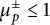$\mu _p^\pm \leq 1$ for all but finitely many primes p with 
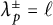$\lambda _p^\pm =\ell $. Assuming a recent conjecture of D. Kundu and A. Ray, our result implies that 
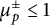$\mu _p^\pm \leq 1$ holds on a density 1 set of good supersingular primes for E.
MSC classification
Primary:
11R23: Iwasawa theory
- Type
- Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society
References
Burungale, A., Skinner, C., Tian, Y., and Wan, X., Zeta elements for elliptic curves and applications. Preprint, 2024. arXiv:2409.01350Google Scholar
Chakravarthy, A., The Iwasawa
$\mu$
-invariants of elliptic curves over
$\mathbb{Q}$
. Preprint, 2024. arXiv:2408.07826
Google Scholar
$\mu$
-invariants of elliptic curves over
$\mathbb{Q}$
. Preprint, 2024. arXiv:2408.07826
Google ScholarChinta, G.,
Analytic ranks of elliptic curves over cyclotomic fields
. J. für Reine Angew. Math. 544(2002), 13–24.Google Scholar
Gajek-Leonard, R., Iwasawa invariants of modular forms with
${a}_p=0$
. Preprint, 2023. arXiv:2302.05748
Google Scholar
${a}_p=0$
. Preprint, 2023. arXiv:2302.05748
Google ScholarGreenberg, R.,
Iwasawa theory for elliptic curves
. In: C. Viola (ed.), Arithmetic theory of elliptic curves (Cetraro, 1997), Lecture Notes in Mathematics, 1716, Springer, Berlin, 1999, pp. 51–144.CrossRefGoogle Scholar
Kato, K.,
p-adic Hodge theory and values of zeta functions of modular forms
. Astérisque 295(2004), 117–290.Google Scholar
Kundu, D. and Ray, A.,
Statistics for iwasawa invariants of elliptic curves
. Trans. Amer. Math. Soc. 374(2021), no. 11, 7945–7965.CrossRefGoogle Scholar
Kobayashi, S.,
Iwasawa theory for elliptic curves at supersingular primes
. Invent. Math. 152(2003), no. 1, 1–36.CrossRefGoogle Scholar
Mazur, B. and Tate, J.,
Refined conjectures of the “Birch and Swinnerton-Dyer type”
. Duke Math. J. 54(1987), no. 2, 711–750.CrossRefGoogle Scholar
Mazur, B., Tate, J., and Teitelbaum, J.,
On
$p$
-adic analogues of the conjectures of Birch and Swinnerton-Dyer
. Invent. Math. 84(1986), no. 1, 1–48.CrossRefGoogle Scholar
$p$
-adic analogues of the conjectures of Birch and Swinnerton-Dyer
. Invent. Math. 84(1986), no. 1, 1–48.CrossRefGoogle ScholarPerrin-Riou, B., Arithmétique des courbes elliptiques à réduction supersingulière en
$p$
. Exp. Math. 12(2003), no. 2, 155–186.CrossRefGoogle Scholar
$p$
. Exp. Math. 12(2003), no. 2, 155–186.CrossRefGoogle ScholarPollack, R.,
On the
$p$
-adic
$L$
-function of a modular form at a supersingular prime. Duke Math. J. 118(2003), no. 3, 523–558.CrossRefGoogle Scholar
$p$
-adic
$L$
-function of a modular form at a supersingular prime. Duke Math. J. 118(2003), no. 3, 523–558.CrossRefGoogle ScholarPollack, R.,
An algebraic version of a theorem of Kurihara
. J. Number Theory 110(2005), pp. 164–177.CrossRefGoogle Scholar
Pollack, R. and Rubin, K.,
The main conjecture for CM elliptic curves at supersingular primes
. Ann. Math. 159(2004), no. 1, 447–464.CrossRefGoogle Scholar
Pollack, R. and Weston, T.,
Mazur-Tate elements of nonordinary modular forms
. Duke Math. J. 156(2011), no. 3, 349–385.CrossRefGoogle Scholar
Sprung, F.,
On pairs of
$p$
-adic
$L$
-functions for weight-two modular forms
. Algebra Number Theory 11(2017), no. 4, 885–928.CrossRefGoogle Scholar
$p$
-adic
$L$
-functions for weight-two modular forms
. Algebra Number Theory 11(2017), no. 4, 885–928.CrossRefGoogle ScholarWashington, L. C., Introduction to cyclotomic fields, Graduate Texts in Mathematics, 83, Springer, New York, 1982.CrossRefGoogle Scholar