Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-09T11:28:56.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Bohr operator on operator-valued polyanalytic functions on simply connected domains

Part of: General theory of linear operators Series expansions Geometric function theory

Published online by Cambridge University Press:  26 June 2023

Vasudevarao Allu Open the ORCID record for Vasudevarao Allu [Opens in a new window]  and
Himadri Halder
Vasudevarao Allu*
Affiliation:
School of Basic Sciences, Indian Institute of Technology Bhubaneswar, Bhubaneswar 752050, India
Himadri Halder
Affiliation:
Mathematics Department, Indian Institute of Technology Bombay, Mumbai 400076, India e-mail: [email protected], [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we study the Bohr operator for the operator-valued subordination class 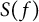$S(f)$ consisting of holomorphic functions subordinate to f in the unit disk 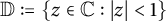$\mathbb {D}:=\{z \in \mathbb {C}: |z|<1\}$, where 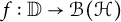$f:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$ is holomorphic and 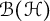$\mathcal {B}(\mathcal {H})$ is the algebra of bounded linear operators on a complex Hilbert space 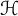$\mathcal {H}$. We establish several subordination results, which can be viewed as the analogs of a couple of interesting subordination results from scalar-valued settings. We also obtain a von Neumann-type inequality for the class of analytic self-mappings of the unit disk 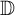$\mathbb {D}$ which fix the origin. Furthermore, we extensively study Bohr inequalities for operator-valued polyanalytic functions in certain proper simply connected domains in 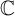$\mathbb {C}$. We obtain Bohr radius for the operator-valued polyanalytic functions of the form 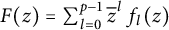$F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $, where 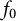$f_{0}$ is subordinate to an operator-valued convex biholomorphic function, and operator-valued starlike biholomorphic function in the unit disk 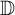$\mathbb {D}$.

Keywords

Banach algebravon Neumann inequalitypolyanalytic functionsBohr operatorsimply connected domains

MSC classification

Primary: 47A56: Functions whose values are linear operators (operator and matrix valued functions, etc., including analytic and meromorphic ones) 30B10: Power series (including lacunary series) 47A63: Operator inequalities
Secondary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 4 , December 2023 , pp. 1411 - 1422
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first-named author is supported by SERB-CRG, and the second-named author is supported by the Institute Postdoctoral Fellowship of IIT Bombay, India.

References

Abdulhadi, Z. and Hajj, L. E., On the univalence of poly-analytic functions . Comput. Methods Funct. Theory 22(2021), 169–181. https://doi.org/10.1007/s40315-021-00378-5.CrossRefGoogle Scholar
Abu Muhanna, Y., Ali, R. M., Ng, Z. C., and Lee, S. K., The Bohr operator on analytic functions and sections . J. Math. Anal. Appl. 496(2021), 124837.CrossRefGoogle Scholar
Agranovsky, M. L., Characterization of polyanalytic functions by meromorphic extensions from chains of circles . J. Anal. Math. 113 (2011), 305–329.CrossRefGoogle Scholar
Ahamed, M. B., Allu, V., and Halder, H., The Bohr phenomenon for analytic functions on shifted disks . Ann. Fenn. Math. 47(2022), 103–120.CrossRefGoogle Scholar
Alkhaleefah, S. A., Kayumov, I. R., and Ponnusamy, S., On the Bohr inequality with a fixed zero coefficient . Proc. Amer. Math. Soc. 147(2019), 5263–5274.CrossRefGoogle Scholar
Allu, V. and Halder, H., Bohr radius for Banach spaces on simply connected domains. Preprint, 2021. https://arxiv.org/pdf/2111.10880.pdf.Google Scholar
BÉnÉteau, C., Dahlner, A., and Khavinson, D., Remarks on the Bohr phenomenon . Comput. Methods Funct. Theory 4(2004), 1–19.CrossRefGoogle Scholar
Aytuna, A. and Djakov, P., Bohr property of bases in the space of entire functions and its generalizations . Bull. Lond. Math. Soc. 45(2013), no. 2, 411–420.CrossRefGoogle Scholar
Balk, M. B., Polyanalytic functions and their generalizations. In: Gonchar, A. A., Havin, V. P., and Nikolski, N. K. (eds.) Complex analysis I, Encyclopedia of Mathematical Sciences, 85, Springer, Berlin, 1997, pp. 195–253.CrossRefGoogle Scholar
Bhowmik, B. and Das, N., Bohr phenomenon for subordinating families of certain univalent functions . J. Math. Anal. Appl. 462(2018), 1087–1098.CrossRefGoogle Scholar
Bhowmik, B. and Das, N., Bohr phenomenon for operator-valued functions . Proc. Edinburgh Math. Soc. 64(2021), no. 1, 72–86. https://doi.org/10.1017/S0013091520000395.CrossRefGoogle Scholar
Boas, H. P. and Khavinson, D., Bohr’s power series theorem in several variables . Proc. Amer. Math. Soc. 125(1997), 2975–2979.CrossRefGoogle Scholar
Bohr, H., A theorem concerning power series . Proc. Lond. Math. Soc. s2–13(1914), 1–5.CrossRefGoogle Scholar
Defant, A., García, D., Maestre, M., and Pérez-García, D., Bohr’s strip for vector valued Dirichlet series . Math. Ann. 342(2008), 533–555.CrossRefGoogle Scholar
Dixon, P. G., Banach algebras satisfying the non-unital von Neumann inequality . Bull. Lond. Math. Soc. 27(1995), no. 4, 359–362.CrossRefGoogle Scholar
Fournier, R. and Ruscheweyh, S., On the Bohr radius for simply connected domains . In: Hilbert spaces of analytic functions, CRM Proceedings and Lecture Notes, 51, American Mathematical Society, Providence, RI, 2010, 165–171.CrossRefGoogle Scholar
Graham, I. and Kohr, G., Geometric function theory in one and higher dimensions, Monographs and Textbooks in Pure and Applied Mathematics, 255, Marcel Dekker, Inc., New York, 2003.CrossRefGoogle Scholar
Hachadi, H. and Youssfi, E. H., The polyanalytic reproducing kernels . Complex Anal. Oper. Theory 13(2019), 3457—3478.CrossRefGoogle Scholar
Hamada, H., Honda, T., and Kohr, G., Bohr’s theorem for holomorphic mappings with values in homogeneous balls . Israel. J. Math. 173(2009), 177–187.CrossRefGoogle Scholar
Kolossov, G. V., Sur les problèmes d’élasticité à deux dimensions. C. R. Acad. Sci. 146 (1908), 522—525.Google Scholar
Paulsen, V. I., Popescu, G., and Singh, D., On Bohr’s inequality . Proc. Lond. Math. Soc. s3–85(2002), 493–512.CrossRefGoogle Scholar
Paulsen, V. I. and Singh, D., Bohr’s inequality for uniform algebras . Proc. Amer. Math. Soc. 132(2002), 3577–3579.CrossRefGoogle Scholar
Paulsen, V. I. and Singh, D., A simple proof of Bohr’s inequality. https://www.math.uh.edu/vern/bohrconf.pdf.Google Scholar
Popescu, G., Bohr inequalities for free holomorphic functions on polyballs . Adv. Math. 347(2019), 1002–1053.CrossRefGoogle Scholar
von Neumann, J., Eine Spektraltheorie für allgemeine Operatoren eines unitären Raumes . Math. Nachr. 4(1951), 258–281.CrossRefGoogle Scholar
Rogosinski, W., On the coefficients of subordinate functions . Proc. Lond. Math. Soc. 48(1943), 48–82.Google Scholar