Published online by Cambridge University Press: 16 December 2019
Block decomposition of 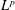 $L^{p}$ spaces with weighted Hausdorff content is established for
$L^{p}$ spaces with weighted Hausdorff content is established for 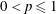 $0<p\leqslant 1$ and the Fefferman–Stein type inequalities are shown for fractional integral operators and some variants of maximal operators.
$0<p\leqslant 1$ and the Fefferman–Stein type inequalities are shown for fractional integral operators and some variants of maximal operators.
Author H. S. is supported by Grant-in-Aid for Young Scientists (19K14577), the Japan Society for the Promotion of Science. Author H. T. is supported by Grant-in-Aid for Scientific Research (C) (15K04918 and 19K03510), the Japan Society for the Promotion of Science.