Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T02:32:04.570Z Has data issue: false hasContentIssue false
  • English
  • Français

The Bifurcation Diagram of Cubic Polynomial Vector Fields on CP1

Published online by Cambridge University Press:  20 November 2018

C. Rousseau
C. Rousseau*
Affiliation:
Department of mathematics and statistics, University of Montreal, C.P. 6128, succ. centre-ville, Montreal, Quebec, H3C 3J7, Canada. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we give the bifurcation diagram of the family of cubic vector fields 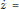$\dot{z}=$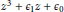${{z}^{3}}+{{\epsilon }_{1}}z+{{\epsilon }_{0}}$ for 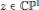$z\in \mathbb{C}{{\mathbb{P}}^{1}}$, depending on the values of 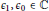${{\epsilon }_{1}},{{\epsilon }_{0}}\in \mathbb{C}$. The bifurcation diagram is in 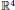${{\mathbb{R}}^{^{4}}}$, but its conic structure allows describing it for parameter values in 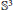${{\mathbb{S}}^{3}}$. There are two open simply connected regions of structurally stable vector fields separated by surfaces corresponding to bifurcations of homoclinic connections between two separatrices of the pole at infinity. These branch from the codimension 2 curve of double singular points. We also explain the bifurcation of homoclinic connection in terms of the description of Douady and Sentenac of polynomial vector fields.

Keywords

34M4532G34complex polynomial vector fieldbifurcation diagramDouady-Sentenac invariant.
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 2 , 01 June 2017 , pp. 381 - 401
Creative Commons
Creative Common License - CCCreative Common License - BY
© Canadian Mathematical Society 2017 This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Branner, B. and Dias, K., Classification of complex polynomial vector fields in one complex variable. J. Difference Equ. Appl. 16(2010), 463–517. http://dx.doi.org/10.1080/10236190903251746 Google Scholar
[2] Douady, A. and Sentenac, P., Champs de vecteurs polynomiaux sur C. Preprint, Paris 2005. (Both authors died before this important visionary work was officially published.)Google Scholar
[3] Hurtubise, J., Lambert, C., and Rousseau, C., Complete system of analytic invariants for unfolded differential linear systems with an irregular singularity ofPoincaré rank k. Mosc. Math. J. 14(2014), no. 2, 309–338, 427. Google Scholar
[4] Lavaurs, P., Systèmes dynamiques holomorphes: explosion de points périodiques paraboliques. Thesis, Université de Paris-Sud, 1989. Google Scholar
[5] Martinet, J., Remarques sur la bifurcation nœud-col dans le domaine complexe. Astérisque 150–51(1987), 131-149. Google Scholar
[6] Mardesic, P., Roussarie, R., and Rousseau, C., Modulus of analytic classification for unfoldings of generic parabolic diffeomorphisms. Mosc. Math. J. 4(2004), 455–502. Google Scholar
[7] Rousseau, C., Analytic moduli for unfoldings of germs of generic analytic diffeomorphisms with a codimension k parabolic point. Ergodic Theory Dynam. Systems 35(2015), no. 1, 274–292. http://dx.doi.org/10.1017/etds.2013.37 Google Scholar
[8] Rousseau, C. and Teyssier, L., Analytical moduli for unfoldings of saddle-node vector-fields. Mosc. Math. J. 8(2008), 547–614.Google Scholar