Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-20T01:08:26.673Z Has data issue: false hasContentIssue false
  • English
  • Français

Biderivations of Lie algebras

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  08 January 2025

Qiufan Chen ,
Yufeng Yao Open the ORCID record for Yufeng Yao [Opens in a new window]  and
Kaiming Zhao Open the ORCID record for Kaiming Zhao [Opens in a new window]
Qiufan Chen
Affiliation:
Department of Mathematics, Shanghai Maritime University, Shanghai, 201306, China
Yufeng Yao*
Affiliation:
Department of Mathematics, Shanghai Maritime University, Shanghai, 201306, China
Kaiming Zhao
Affiliation:
Department of Mathematics, Wilfrid Laurier University, Waterloo, ON, Canada N2L 3C5, and School of Mathematical Science, Hebei Normal (Teachers) University, Shijiazhuang, Hebei, 050024, China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we first introduce the concept of symmetric biderivation radicals and characteristic subalgebras of Lie algebras and study their properties. Based on these results, we precisely determine biderivations of some Lie algebras including finite-dimensional simple Lie algebras over arbitrary fields of characteristic not 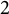$2$ or $3$, and the Witt algebras $\mathcal {W}^+_n$ over fields of characteristic $0$. As an application, commutative post-Lie algebra structure on the aforementioned Lie algebras is shown to be trivial.

Keywords

Symmetric biderivationWitt algebrafinite-dimensional simple Lie algebrasymmetric radicalcharacteristic subalgebra

MSC classification

Primary: 17B20: Simple, semisimple, reductive (super)algebras 17B40: Automorphisms, derivations, other operators 17B65: Infinite-dimensional Lie (super)algebras 17B66: Lie algebras of vector fields and related (super) algebras
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by the National Natural Science Foundation of China (Grant Nos. 12271345 and 12071136) and NSERC (311907-2020).

References

Benkart, G., Gregory, T., and Premet, A., The recognition theorem for graded Lie algebras in prime characteristic . Mem. Am. Math. Soc. 920(2009), 1–145.Google Scholar
Benkovic, D., Biderivations of triangular algebras . Linear Algebra Appl. 431(2009), 1587–1602.CrossRefGoogle Scholar
Brešar, M., On generalized biderivations and related maps . J. Algebra 172(1995), 764–786.CrossRefGoogle Scholar
Brešar, M., Near-derivations in Lie algebras . J. Algebra 320(2008), 3765–3772.CrossRefGoogle Scholar
Brešar, M., Martindale, W. S., and Miers, C. R., Centralizing maps in prime rings with involution . J. Algebra 161(1993), 342–357.CrossRefGoogle Scholar
Brešar, M. and Zhao, K., Biderivations and commuting linear maps on Lie algebras . J. Lie Theory 28(2018), 885–900.Google Scholar
Burde, D., Left-symmetric algebras, or pre-Lie algebras in geometry and physics . Cent. Eur. J. Math. 4(2006), no. 3, 323–357.Google Scholar
Burde, D. and Dekimpe, K., Post-Lie algebra structures on pairs of Lie algebras . J. Algebra 464(2016), 226–245.CrossRefGoogle Scholar
Burde, D. and Moens, W. A., Commutative post-Lie algebra structures on Lie algebras . J. Algebra 467(2016), 183–201.CrossRefGoogle Scholar
Carter, R., Lie algebras of finite and affine type, Cambridge University Press, Cambridge, 2005.CrossRefGoogle Scholar
Collingwood, D. H. and McGovern, W. M., Nilpotent orbits in semisimple lie algebras, Van Nostrand, New York, 1993.Google Scholar
Dilxat, M., Gao, S., and Liu, D., Super-biderivations and post-Lie superalgebras on some Lie superalgebras . Acta Math. Sin. 39(2023), no. 9, 1736–1754.CrossRefGoogle Scholar
Dokovic, D. Z. and Zhao, K., Generalized Cartan type W Lie algebras in characteristic zero . J. Algebra 195(1997), 170–210.CrossRefGoogle Scholar
Du, Y. and Wang, Y., Biderivations of generalized matrix algebras . Linear Algebra Appl. 438(2013), no. 11, 4483–4499.CrossRefGoogle Scholar
Ebrahimi-Fard, K., Lundervold, A., Mencattini, I., and Munthe-Kaas, H., Post-Lie algebras and isospectral flows . SIGMA Sym. Integr. Geom. Methods Appl. 11(2015), 093.Google Scholar
Humphreys, J. E., Introduction to Lie algebras and representation theory, Springer Science Business Media, Berlin, 1972.CrossRefGoogle Scholar
Jacobson, N., Lie algebras, Interscience Tracts in Pure and Applied Mathematics, No. 10, Interscience Publishers (a division of John Wiley & Sons, Inc.), New York and London, 1962, ix+331 pp.Google Scholar
Leger, F. and Luks, E., Generalized derivations of Lie algebras . J. Algebra 228(2000), 165–203.CrossRefGoogle Scholar
Liu, X., Guo, X., and Zhao, K., Biderivations of block Lie algebras . Linear Algebra Appl. 538(2018), 43–55.CrossRefGoogle Scholar
Loday, J. L., Generalized bialgebras and triples of operads . Astérisque 320(2008), 116 pp.Google Scholar
Tang, X., Biderivations of finite-dimensional complex simple Lie algebras . Linear Multilinear A. 66(2018), no. 2, 250–259.CrossRefGoogle Scholar
Tang, X., Biderivations, commuting maps and commutative post-Lie algebra structures on $W$ -algebras . Commun. Algebra 45(2017), no. 12, 5252–5261.CrossRefGoogle Scholar
Tang, X. and Yang, Y., Biderivations of the higher rank Witt algebra without anti-symmetric condition . Open Math. 16(2018), 447–452.CrossRefGoogle Scholar
Vallette, B., Homology of generalized partition posets . J. Pure Appl. Algebra 208(2007), 699–725.CrossRefGoogle Scholar
Wang, D. and Yu, X., Biderivations and linear commuting maps on the Schrödinger–Virasoro Lie algebra . Commun. Algebra 41(2013), 2166–2173.CrossRefGoogle Scholar
Wang, D., Yu, X., and Chen, Z., Biderivations of parabolic subalgebras of simple Lie algebras . Commun. Algebra 39(2011), 4097–4104.CrossRefGoogle Scholar
Xia, C., Wang, D., and Han, X., Linear super-commuting maps and super-biderivations on the super-Virasoro algebras . Commun. Algebra 44(2016), 5342–5350.CrossRefGoogle Scholar
Zhang, J., Feng, S., Li, H., and Wu, R., Generalized biderivations of nest algebras . Linear Algebra Appl. 418(2006), 225–233.CrossRefGoogle Scholar