Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T03:06:29.382Z Has data issue: false hasContentIssue false
  • English
  • Français

Betti Numbers and Flat Dimensions of Local Cohomology Modules

Published online by Cambridge University Press:  20 November 2018

Alireza Vahidi
Alireza Vahidi*
Affiliation:
Department of Mathematics, Payame Noor University (PNU), IRAN e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Assume that 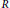$R$ is a commutative Noetherian ring with non-zero identity, $\mathfrak{a}$ is an ideal of 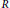$R$, and 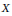$X$ is an 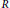$R$-module. In this paper, we first study the finiteness of Betti numbers of local cohomology modules 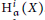$\text{H}_{\mathfrak{a}}^{i}\left( X \right)$. Then we give some inequalities between the Betti numbers of 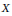$X$ and those of its local cohomology modules. Finally, we present many upper bounds for the flat dimension of 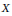$X$ in terms of the flat dimensions of its local cohomology modules and an upper bound for the flat dimension of 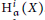$\text{H}_{\mathfrak{a}}^{i}\left( X \right)$ in terms of the flat dimensions of the modules 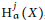$\text{H}_{\mathfrak{a}}^{j}\left( X \right),j\ne i$, and that of 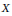$X$.

Keywords

13D4513D05Betti numbersflat dimensionslocal cohomology modules
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 3 , 01 September 2015 , pp. 664 - 672
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Aghapournahr, M., Taherizadeh, A. J., and Vahidi, A., Extension functors of local cohomology modules. Bull. Iran. Math. Soc. 37(2011), no. 3,117–134.Google Scholar
[2] Brodmann, M. P. and Sharp, R. Y., Local cohomology: an algebraic introduction with geometric applications. Cambridge Studies in Advanced Mathematics, 60, Cambridge University Press, Cambridge, 1998.Google Scholar
[3] Bruns, W. and Herzog, J., Cohen-Macaulay rings. Cambridge Studies in Advanced Mathematics, 39, Cambridge University Press, Cambridge, 1993.Google Scholar
[4] Delfino, D. and Marley, T., Cofinite modules and local cohomology. J. Pure Appl. Algebra 121(1997), no. 1, 45–52. http://dx.doi.Org/10.101 6/S0022-4049(96)00044-8 Google Scholar
[5] Dibaei, M. T. and Vahidi, A., Artinian and non-Artinian local cohomology modules. Canad. Math. Bull. 54(2011), no. 4, 619–629. http://dx.doi.org/10.4153/CMB-2011-042-5 Google Scholar
[6] Dibaei, M. T. and Vahidi, A., Torsion functors of local cohomology modules. Algebr. Represent. Theory 14(2011), no. 1, 79–85. http://dx.doi.Org/10.1007/s10468-009-91 77-y Google Scholar
[7] Dibaei, M. T. and Yassemi, S., Bass numbers of local cohomology modules with respect to an ideal. Algebr. Represent. Theory H(2008), no. 3, 299–306. http://dx.doi.Org/10.1007/s10468-007-9072-3 Google Scholar
[8] Hartshorne, R., Cohomological dimension of algebraic varieties. Ann. of Math. 88(1968), 403–450. http://dx.doi.Org/10.2307/1 970720 Google Scholar
[9] Hassanzadeh, S. H. and Vahidi, A. On vanishing and cofiniteness of generalized local cohomologymodules. Commun. Algebra 37(2009), no. 7, 2290–2299. http://dx.doi.org/10.1080/00927870802 622718 Google Scholar
[10] Kawasaki, K., On the finiteness of Bass numbers of local cohomology modules. Proc. Amer. Math. Soc. 124(1996), no. 11, 3275–3279. http://dx.doi.org/10.1090/S0002-9939-96-03399-0 Google Scholar
[11] Rotman, J., An introduction to homological algebra. Pure and Applied Mathematics, 85, Academic Press, New York-London, 1979.Google Scholar