Published online by Cambridge University Press: 20 November 2018
If K is a triangulation of a closed 3-manifold M with E0(K) edges and F0(K) triangles, then the average edge order of K is defined to be
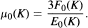
In [8], the relations between this quantity and the topology of M are investigated, especially in the case of μ0(K) being small (where the study relies on Oda's classification of triangulations of 𝕊2 up to eight vertices—see [9]). In the present paper, the attention is fixed upon the average edge order of coloured triangulations; surprisingly enough, the obtained results are perfectly analogous to Luo-Stong' ones, and may be proved with little effort by means of edge-coloured graphs representing manifolds.