Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T06:16:49.247Z Has data issue: false hasContentIssue false
  • English
  • Français

Auslander-Reiten Sequences for "Nice" Torsion Theories of Artinian Algebras

Published online by Cambridge University Press:  20 November 2018

K. W. Roggenkamp
K. W. Roggenkamp*
Affiliation:
Mathematisches Institut B Universitat Stuttgart 7 Stuttgart 1, Postfach 560, West Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

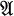Let t be a field and a finite dimensional t-algebra. Auslander-Reiten sequences [AR] play a fundamental rôle in the representation theory of 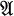; in particular, they can be used to construct new indecomposable modules from known ones. For the latter reason I think it worthwile to point out certain torsion theories 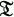on the category of 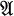-modules, such that the category of 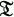-torsionfree modules has Auslander-Reiten sequences; thus giving another construction of indecomposable modules.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 23 , Issue 1 , 01 March 1980 , pp. 61 - 65
Copyright
Copyright © Canadian Mathematical Society 1980

References

[A] Auslander, M., Existence theorems for almost split sequences, Oklahoma Ring theory conference, March 1976.Google Scholar
Auslander, M., Representation theory of Artin algebras I, II, Comm. Algebra, 1, 177-268 (1974), 1, 239-294 (1975).Google Scholar
[AP] Auslander, M. and Platzeck, I. M., Representation theory of hereditary Artin algebras, Preprint 1976.Google Scholar
[AR] Auslander, M. and Reiten, I., Representation theory of Artin algebras III, Comm. Algebra 3, 239-294 (1975).Google Scholar
[DR] Dlab, V. and Ringel, C. M., Indecomposable representations of graphs and algebras, Memoir Am. Math. Soc. 173, 1976.Google Scholar
[Rl] Roggenkamp, K. W., The construction of almost split sequences for integral group rings and orders, Comm. Algebra 5, 1363-1373.Google Scholar
[R2] Roggenkamp, K. W., Some examples of orders of global dimension two, Math. Z. 154, 225-238 (1977).Google Scholar
Roggenkamp, K. W., Orders of global dimension two, Math. Z. 160, 63-67, (1978).Google Scholar
[R3] Roggenkamp, K. W., Indecomposable representations of orders of global dimension two II, to appear J. Algebra.Google Scholar
[RR1] Ringel, C. M. and Roggenkamp, K. W., Diagrammatic methods in representation theory of orders, to appear J. Algebra.Google Scholar
[RR2] Ringel, C. M. and Roggenkamp, K. W., Indecomposable representations of orders of global dimension two I, to be published.Google Scholar
[S] Stenstrom, B., Rings of quotients, Grundl. Math. 217, Springer-Verlag 1975.Google Scholar