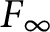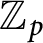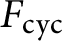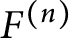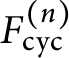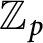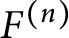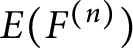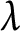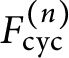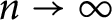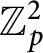1 Introduction
The Mordell–Weil Theorem states that given an elliptic curve E defined over a number field F, its F-rational points form a finitely generated abelian group, i.e.,
where r is a non-negative integer called the Mordell–Weil rank. In [Reference Mazur22], Mazur initiated the study of Selmer groups of elliptic curves in
![]() $\mathbb {Z}_p$
-extensions. A major application of Iwasawa theory is the study of the growth of Mordell–Weil ranks of abelian varieties in towers of number fields. Given an abelian variety defined over a number field F with good ordinary reduction at the primes above p, Mazur showed that the rank of A is bounded in the cyclotomic
$\mathbb {Z}_p$
-extensions. A major application of Iwasawa theory is the study of the growth of Mordell–Weil ranks of abelian varieties in towers of number fields. Given an abelian variety defined over a number field F with good ordinary reduction at the primes above p, Mazur showed that the rank of A is bounded in the cyclotomic
![]() $\mathbb {Z}_p$
-extension of F. Kato and Rohlrich proved the analogous statement for all elliptic curves defined over abelian number fields, see [Reference Kato15, Reference Rohrlich24]. Alongside further developments in Iwasawa theory over larger p-adic Lie extensions, there has been significant interest in analyzing the asymptotic growth of Mordell–Weil ranks in towers. For ordinary primes, Mazur in [Reference Mazur23] formulated a precise conjecture on the growth of ranks in any
$\mathbb {Z}_p$
-extension of F. Kato and Rohlrich proved the analogous statement for all elliptic curves defined over abelian number fields, see [Reference Kato15, Reference Rohrlich24]. Alongside further developments in Iwasawa theory over larger p-adic Lie extensions, there has been significant interest in analyzing the asymptotic growth of Mordell–Weil ranks in towers. For ordinary primes, Mazur in [Reference Mazur23] formulated a precise conjecture on the growth of ranks in any
![]() $\mathbb {Z}_p$
-extension of an imaginary quadratic field F, called the Growth number conjecture. This question has been studied in anticyclotomic extensions by Cornut [Reference Cornut4] and Vatsal [Reference Vatsal26]. A prototypical example of interest is the
$\mathbb {Z}_p$
-extension of an imaginary quadratic field F, called the Growth number conjecture. This question has been studied in anticyclotomic extensions by Cornut [Reference Cornut4] and Vatsal [Reference Vatsal26]. A prototypical example of interest is the
![]() $\mathbb {Z}_p^2$
-extension
$\mathbb {Z}_p^2$
-extension
![]() $F_\infty $
of an imaginary quadratic field F. For every integer
$F_\infty $
of an imaginary quadratic field F. For every integer
![]() $n\geq 1$
, set
$n\geq 1$
, set
![]() $F^{(n)}$
to denote the nth layer. In this setting, it is the extension contained in
$F^{(n)}$
to denote the nth layer. In this setting, it is the extension contained in
![]() $F_\infty $
such that
$F_\infty $
such that
 $\operatorname {Gal}(F^{(n)}/F)=\left (\mathbb {Z}/p^n\mathbb {Z}\right )^2$
. For elliptic curves
$\operatorname {Gal}(F^{(n)}/F)=\left (\mathbb {Z}/p^n\mathbb {Z}\right )^2$
. For elliptic curves
![]() $E_{/F}$
, asymptotic formulas for the growth of the rank of
$E_{/F}$
, asymptotic formulas for the growth of the rank of
![]() $E(F^{(n)})$
as
$E(F^{(n)})$
as
![]() $n\rightarrow \infty $
have been proven by Lei and Sprung in [Reference Lei and Sprung19]. More recently, such growth questions are studied in admissible uniform pro-p extensions of number fields by Delbourgo and Lei in [Reference Delbourgo and Lei7], and by Hung and Lim in [Reference Hung and Lim14].
$n\rightarrow \infty $
have been proven by Lei and Sprung in [Reference Lei and Sprung19]. More recently, such growth questions are studied in admissible uniform pro-p extensions of number fields by Delbourgo and Lei in [Reference Delbourgo and Lei7], and by Hung and Lim in [Reference Hung and Lim14].
In this note, we employ a new strategy to study the growth of ranks in noncommutative towers. Let
 $F^{(n)}_{\operatorname {cyc}}$
be the cyclotomic
$F^{(n)}_{\operatorname {cyc}}$
be the cyclotomic
![]() $\mathbb {Z}_p$
-extension of
$\mathbb {Z}_p$
-extension of
![]() $F^{(n)}$
. We study the growth of the rank of
$F^{(n)}$
. We study the growth of the rank of
![]() $E(F^{(n)})$
by analyzing the growth of the
$E(F^{(n)})$
by analyzing the growth of the
![]() $\lambda $
-invariant of the Selmer group over
$\lambda $
-invariant of the Selmer group over
 $F^{(n)}_{ \operatorname {cyc}}$
as
$F^{(n)}_{ \operatorname {cyc}}$
as
![]() $n\rightarrow \infty $
using a generalizations of Kida’s formula due to Hachimori and Matsuno [Reference Hachimori and Matsuno11] and Lim [Reference Lim20]. The method has several advantages. First, it is a straightforward application of Kida’s formula which a priori allows one to circumvent technicalities of noncommutative Iwasawa theory. In other words, the proof is short and can be understood without familiarity with methods in noncommutative Iwasawa theory, though it does build on previous work of Lim [Reference Lim21] which uses nontrivial results in the subject. Given an elliptic curve E over a number field F, we do however require that the Selmer group of E over the cyclotomic
$n\rightarrow \infty $
using a generalizations of Kida’s formula due to Hachimori and Matsuno [Reference Hachimori and Matsuno11] and Lim [Reference Lim20]. The method has several advantages. First, it is a straightforward application of Kida’s formula which a priori allows one to circumvent technicalities of noncommutative Iwasawa theory. In other words, the proof is short and can be understood without familiarity with methods in noncommutative Iwasawa theory, though it does build on previous work of Lim [Reference Lim21] which uses nontrivial results in the subject. Given an elliptic curve E over a number field F, we do however require that the Selmer group of E over the cyclotomic
![]() $\mathbb {Z}_p$
-extension of F be cotorsion over the Iwasawa algebra and impose the
$\mathbb {Z}_p$
-extension of F be cotorsion over the Iwasawa algebra and impose the
![]() $\mathfrak {M}_H(G)$
conjecture (see [Reference Coates and Sujatha2, Reference Lim20]).
$\mathfrak {M}_H(G)$
conjecture (see [Reference Coates and Sujatha2, Reference Lim20]).
Secondly, (and perhaps more importantly) the method strengthens known results and these estimates are closer to conjectured asymptotics. The error term in the asymptotic formulas of Hung–Lim are removed in the process, and the main term is sharper (see Remark 2.8 for further details). The significance of this is illustrated for certain examples, namely,
![]() $\mathbb {Z}_p^d$
-extensions, false Tate-curve extensions, and trivializing extensions generated by the p-primary torsion of a non-CM elliptic curve. It should be pointed out here that for
$\mathbb {Z}_p^d$
-extensions, false Tate-curve extensions, and trivializing extensions generated by the p-primary torsion of a non-CM elliptic curve. It should be pointed out here that for
![]() $\mathbb {Z}_p^2$
-extensions, a similar question was studied by Cuoco in [Reference Cuoco6], who studied the growth of Iwasawa invariants associated with class group towers in families of
$\mathbb {Z}_p^2$
-extensions, a similar question was studied by Cuoco in [Reference Cuoco6], who studied the growth of Iwasawa invariants associated with class group towers in families of
![]() $\mathbb {Z}_p$
-extensions contained in the composite of two
$\mathbb {Z}_p$
-extensions contained in the composite of two
![]() $\mathbb {Z}_p$
-extensions. The results can also be applied to prove statistical results.
$\mathbb {Z}_p$
-extensions. The results can also be applied to prove statistical results.
-
(1) In Corollary 3.3, it is shown that if E is an elliptic curve defined over an imaginary quadratic field F such that E does not have complex multiplication and
 $\operatorname {rank}E(F)=0$
, then the rank remains 0 is
$\operatorname {rank}E(F)=0$
, then the rank remains 0 is
 $100\%$
of
$100\%$
of
 $\mathbb {Z}_p^2$
-extensions of F.
$\mathbb {Z}_p^2$
-extensions of F. -
(2) In Corollary 3.7, we consider the curve
 $E=$
11a2. It is shown that there is a positive density set of primes
$E=$
11a2. It is shown that there is a positive density set of primes
 $\ell $
such that for all integers
$\ell $
such that for all integers $$ \begin{align*}\operatorname{rank}E\left(\mathbb{Q}(\mu_{7^{n+1}}, \ell^{\frac{1}{7^n}})\right)\leq \lambda_7(E/\mathbb{Q}(\mu_{7^\infty}))7^n\end{align*} $$
$$ \begin{align*}\operatorname{rank}E\left(\mathbb{Q}(\mu_{7^{n+1}}, \ell^{\frac{1}{7^n}})\right)\leq \lambda_7(E/\mathbb{Q}(\mu_{7^\infty}))7^n\end{align*} $$
 $n>0$
.
$n>0$
.
The method employed in this paper shows that in any context in which a satisfactory generalization of Kida’s formula is proved, it should be possible to analyze the growth of
![]() $\lambda $
-invariants in noncommutative towers. We point out that analogs of Kida’s formula have been proven for fine Selmer groups by Kundu in [Reference Kundu17]. In this particular context, the number fields are assumed to be totally real. Also, such results were proved by Hatley and Lei in the supersingular setting, see [Reference Hatley and Lei13].
$\lambda $
-invariants in noncommutative towers. We point out that analogs of Kida’s formula have been proven for fine Selmer groups by Kundu in [Reference Kundu17]. In this particular context, the number fields are assumed to be totally real. Also, such results were proved by Hatley and Lei in the supersingular setting, see [Reference Hatley and Lei13].
2 Growth of Iwasawa invariants in towers
In this section, we introduce some preliminary notions and prove the main result of this paper.
2.1 Uniform pro-
 $p$
extensions
$p$
extensions
Throughout, p will be a prime
![]() $\geq 5$
and F a number field. Let
$\geq 5$
and F a number field. Let
![]() $F_\infty $
be an infinite Galois extension of F with pro-p Galois group
$F_\infty $
be an infinite Galois extension of F with pro-p Galois group
![]() $G:=\operatorname {Gal}(F_\infty /F)$
. The lower central p-series of G is recursively defined as follows:
$G:=\operatorname {Gal}(F_\infty /F)$
. The lower central p-series of G is recursively defined as follows:
Definition 2.1 The group G is said to be uniform if
-
(1) it is finitely generated,
-
(2) it is powerful, i.e.,
 $[G,G]\subseteq G^p$
, and
$[G,G]\subseteq G^p$
, and -
(3)
 $[G_n:G_{n+1}]=[G:G_1]$
for all
$[G_n:G_{n+1}]=[G:G_1]$
for all
 $n\in \mathbb {Z}_{\geq 1}$
.
$n\in \mathbb {Z}_{\geq 1}$
.
Setting
![]() $d:=[G:G_1]$
, we observe that
$d:=[G:G_1]$
, we observe that
![]() $[G:G_n]=p^{dn}$
. Assume that G has the structure of a p-adic Lie group. We say that
$[G:G_n]=p^{dn}$
. Assume that G has the structure of a p-adic Lie group. We say that
![]() $F_\infty $
is a strongly admissible p-adic Lie extension if
$F_\infty $
is a strongly admissible p-adic Lie extension if
-
(1) only finitely many primes ramify in
 $F_\infty $
,
$F_\infty $
, -
(2)
 $F_\infty $
contains the cyclotomic
$F_\infty $
contains the cyclotomic
 $\mathbb {Z}_p$
-extension
$\mathbb {Z}_p$
-extension
 $F_{\operatorname {cyc}}$
of F, and
$F_{\operatorname {cyc}}$
of F, and -
(3) the p-torsion subgroup of G is trivial.
We assume that
![]() $F_\infty $
is pro-p a strongly admissible p-adic Lie extension and G is uniform. Note that
$F_\infty $
is pro-p a strongly admissible p-adic Lie extension and G is uniform. Note that
 $G_{n}/G_{n+1}\simeq \left (\mathbb {Z}/p\mathbb {Z}\right )^d$
for
$G_{n}/G_{n+1}\simeq \left (\mathbb {Z}/p\mathbb {Z}\right )^d$
for
![]() $n\in \mathbb {Z}_{\geq 1}$
. It is well known that the dimension of G is equal to d and that
$n\in \mathbb {Z}_{\geq 1}$
. It is well known that the dimension of G is equal to d and that
![]() $G_n=G^{p^n}$
, see [Reference Dixon, Du Sautoy, Mann and Segal8, Theorem 3.6]. The extension
$G_n=G^{p^n}$
, see [Reference Dixon, Du Sautoy, Mann and Segal8, Theorem 3.6]. The extension
![]() $F_\infty $
is filtered by a tower of number fields. Setting
$F_\infty $
is filtered by a tower of number fields. Setting
![]() $F^{(n)}:=F_\infty ^{G_n}$
, consider the nonabelian tower
$F^{(n)}:=F_\infty ^{G_n}$
, consider the nonabelian tower
and let
 $F^{(n)}_{\operatorname {cyc}}$
be the cyclotomic
$F^{(n)}_{\operatorname {cyc}}$
be the cyclotomic
![]() $\mathbb {Z}_p$
-extension of
$\mathbb {Z}_p$
-extension of
![]() $F^{(n)}$
. We have thus filtered the extension
$F^{(n)}$
. We have thus filtered the extension
![]() $F_\infty $
into a tower of cyclotomic
$F_\infty $
into a tower of cyclotomic
![]() $\mathbb {Z}_p$
-extensions
$\mathbb {Z}_p$
-extensions
 $$ \begin{align*}F_{\operatorname{cyc}}=F^{(0)}_{\operatorname{cyc}}\subset F^{(1)}_{\operatorname{cyc}}\subset \cdots \subset F^{(n)}_{\operatorname{cyc}}\subset \cdots\end{align*} $$
$$ \begin{align*}F_{\operatorname{cyc}}=F^{(0)}_{\operatorname{cyc}}\subset F^{(1)}_{\operatorname{cyc}}\subset \cdots \subset F^{(n)}_{\operatorname{cyc}}\subset \cdots\end{align*} $$
Set
![]() $H:=\operatorname {Gal}(F_\infty /F_{\operatorname {cyc}})$
and
$H:=\operatorname {Gal}(F_\infty /F_{\operatorname {cyc}})$
and
![]() $\Gamma :=G/H\simeq \mathbb {Z}_p$
. For
$\Gamma :=G/H\simeq \mathbb {Z}_p$
. For
![]() $n\in \mathbb {Z}_{\geq 1}$
, we write
$n\in \mathbb {Z}_{\geq 1}$
, we write
![]() $H_n$
(resp.
$H_n$
(resp.
![]() $\Gamma _n$
) for the descending central series of H (resp.
$\Gamma _n$
) for the descending central series of H (resp.
![]() $\Gamma $
). We list a few useful facts.
$\Gamma $
). We list a few useful facts.
Lemma 2.2 The following assertions hold:
-
(1) The normal subgroup H is uniform with
 $(d-1)$
generators, and
$(d-1)$
generators, and
 $H_n$
is identified with
$H_n$
is identified with
 $H\cap G_n$
.
$H\cap G_n$
. -
(2)
 $\Gamma _n$
is identified with
$\Gamma _n$
is identified with
 $G_n/H_n$
.
$G_n/H_n$
.
Proof See [Reference Dixon, Du Sautoy, Mann and Segal8, Theorem 3.6] and [Reference Hung and Lim14, Lemma 2.6] for further details.▪
As a result, we have that
 $F^{(n)}_{\operatorname {cyc}}=F_\infty ^{H_n}$
and hence,
$F^{(n)}_{\operatorname {cyc}}=F_\infty ^{H_n}$
and hence,
 $$ \begin{align*}\operatorname{Gal}(F^{(n+1)}_{\operatorname{cyc}}/F^{(n)}_{\operatorname{cyc}})=H_n/H_{n+1}\simeq \left(\mathbb{Z}/p\mathbb{Z}\right)^{d-1}.\end{align*} $$
$$ \begin{align*}\operatorname{Gal}(F^{(n+1)}_{\operatorname{cyc}}/F^{(n)}_{\operatorname{cyc}})=H_n/H_{n+1}\simeq \left(\mathbb{Z}/p\mathbb{Z}\right)^{d-1}.\end{align*} $$
Since
![]() $\Gamma _n=G_n/H_n$
, we have that
$\Gamma _n=G_n/H_n$
, we have that
 $\Gamma _n=\operatorname {Gal}(F^{(n)}_{\operatorname {cyc}}/F^{(n)})$
. We now introduce the Iwasawa-algebra at the nth level, taken to be
$\Gamma _n=\operatorname {Gal}(F^{(n)}_{\operatorname {cyc}}/F^{(n)})$
. We now introduce the Iwasawa-algebra at the nth level, taken to be
 $$ \begin{align*}\Lambda(\Gamma_n):=\varprojlim_L \mathbb{Z}_p[\operatorname{Gal}(L/F^{(n)})],\end{align*} $$
$$ \begin{align*}\Lambda(\Gamma_n):=\varprojlim_L \mathbb{Z}_p[\operatorname{Gal}(L/F^{(n)})],\end{align*} $$
where L ranges over all number fields contained in between
![]() $F^{(n)}$
and
$F^{(n)}$
and
 $F^{(n)}_{\operatorname {cyc}}$
. Choose a topological generator
$F^{(n)}_{\operatorname {cyc}}$
. Choose a topological generator
![]() $\gamma _n$
of
$\gamma _n$
of
![]() $\Gamma _n$
and fix the isomorphism
$\Gamma _n$
and fix the isomorphism
![]() sending
sending
![]() $\gamma _n-1$
to x.
$\gamma _n-1$
to x.
More generally, if
![]() $\mathcal {G}$
is any pro-p group, set
$\mathcal {G}$
is any pro-p group, set
 $$ \begin{align*}\Lambda(\mathcal{G}):=\varprojlim_U \mathbb{Z}_p[\mathcal{G}/U],\end{align*} $$
$$ \begin{align*}\Lambda(\mathcal{G}):=\varprojlim_U \mathbb{Z}_p[\mathcal{G}/U],\end{align*} $$
where U ranges over all finite index normal subgroups of
![]() $\mathcal {G}$
. Given a number field F, we set
$\mathcal {G}$
. Given a number field F, we set
 $\Lambda _F:=\Lambda \left (\operatorname {Gal}(F_{\operatorname {cyc}}/F)\right )$
.
$\Lambda _F:=\Lambda \left (\operatorname {Gal}(F_{\operatorname {cyc}}/F)\right )$
.
2.2 Iwasawa invariants
Let M be a cofinitely generated cotorsion
-module, i.e., the Pontryagin-dual
![]() $M^{\vee }:=\operatorname {Hom}(M, \mathbb {Q}_p/\mathbb {Z}_p)$
is a finitely generated and torsion
$M^{\vee }:=\operatorname {Hom}(M, \mathbb {Q}_p/\mathbb {Z}_p)$
is a finitely generated and torsion
-module. Recall that a polynomial
is said to be distinguished if it is a monic polynomial whose nonleading coefficients are all divisible by p. Note that all height
![]() $1$
prime ideals of
$1$
prime ideals of
are principal ideals
![]() $(a)$
, where
$(a)$
, where
![]() $a=p$
or
$a=p$
or
![]() $a=f(x)$
, where
$a=f(x)$
, where
![]() $f(x)$
is an irreducible distinguished polynomial. According to the structure theorem for
$f(x)$
is an irreducible distinguished polynomial. According to the structure theorem for
-modules (see [Reference Washington27, Theorem 13.12]),
![]() $M^{\vee }$
is pseudo-isomorphic to a finite direct sum of cyclic
$M^{\vee }$
is pseudo-isomorphic to a finite direct sum of cyclic
-modules, i.e., there is a map

with finite kernel and cokernel. Here,
![]() $\mu _i>0$
,
$\mu _i>0$
,
![]() $e_j>0$
, and
$e_j>0$
, and
![]() $g_j(x)$
is an irreducible distinguished polynomial. Furthermore, the numbers
$g_j(x)$
is an irreducible distinguished polynomial. Furthermore, the numbers
![]() $\mu _1, \dots , \mu _s$
and irreducible distinguished polynomials
$\mu _1, \dots , \mu _s$
and irreducible distinguished polynomials
![]() $g_1(x),\dots , g_t(x)$
are uniquely determined. The characteristic ideal of
$g_1(x),\dots , g_t(x)$
are uniquely determined. The characteristic ideal of
![]() $M^\vee $
is (up to a unit) generated by
$M^\vee $
is (up to a unit) generated by
 $$ \begin{align*} f_{M}^{(p)}(x) = f_{M}(x) := p^{\sum_{i} \mu_i} \prod_j g_j^{e_j}(x). \end{align*} $$
$$ \begin{align*} f_{M}^{(p)}(x) = f_{M}(x) := p^{\sum_{i} \mu_i} \prod_j g_j^{e_j}(x). \end{align*} $$
The
![]() $\mu $
-invariant of M is defined as the power of p in
$\mu $
-invariant of M is defined as the power of p in
![]() $f_{M}(x)$
. More precisely,
$f_{M}(x)$
. More precisely,
 $$ \begin{align*} \mu_p(M):=\begin{cases} \sum_{i=1}^s \mu_i & \textrm{ if } s>0,\\ 0 & \textrm{ if } s=0. \end{cases} \end{align*} $$
$$ \begin{align*} \mu_p(M):=\begin{cases} \sum_{i=1}^s \mu_i & \textrm{ if } s>0,\\ 0 & \textrm{ if } s=0. \end{cases} \end{align*} $$
The
![]() $\lambda $
-invariant of M is the degree of the characteristic element, i.e.,
$\lambda $
-invariant of M is the degree of the characteristic element, i.e.,
 $$ \begin{align*} \lambda_p(M) :=\begin{cases} \sum_{i=1}^t e_i\deg g_i & \textrm{ if } s>0,\\ 0 & \textrm{ if } s=0. \end{cases} \end{align*} $$
$$ \begin{align*} \lambda_p(M) :=\begin{cases} \sum_{i=1}^t e_i\deg g_i & \textrm{ if } s>0,\\ 0 & \textrm{ if } s=0. \end{cases} \end{align*} $$
Since the numbers
![]() $\mu _i$
and polynomials
$\mu _i$
and polynomials
![]() $g_j(x)$
are uniquely determined by M, the
$g_j(x)$
are uniquely determined by M, the
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
-invariants determined above are well defined.
$\lambda $
-invariants determined above are well defined.
Let F be a number field and E an elliptic curve over F with good ordinary reduction at all primes of F above p. Denote by
![]() $\operatorname {Sel}_{p^\infty }(E/F_{\operatorname {cyc}})$
the p-primary Selmer group of E over
$\operatorname {Sel}_{p^\infty }(E/F_{\operatorname {cyc}})$
the p-primary Selmer group of E over
![]() $F_{\operatorname {cyc}}$
(see [Reference Coates and Sujatha1] for further details). Suppose
$F_{\operatorname {cyc}}$
(see [Reference Coates and Sujatha1] for further details). Suppose
![]() $\operatorname {Sel}_{p^\infty }(E/F_{\operatorname {cyc}})$
that is a cotorsion
$\operatorname {Sel}_{p^\infty }(E/F_{\operatorname {cyc}})$
that is a cotorsion
![]() $\Lambda _F$
-module, we set
$\Lambda _F$
-module, we set
![]() $\mu _p(E/F)$
and
$\mu _p(E/F)$
and
![]() $\lambda _p(E/F)$
to denote the
$\lambda _p(E/F)$
to denote the
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
-invariant of
$\lambda $
-invariant of
![]() $\operatorname {Sel}_{p^\infty }(E/F_{\operatorname {cyc}})$
respectively, when viewed as a module over
$\operatorname {Sel}_{p^\infty }(E/F_{\operatorname {cyc}})$
respectively, when viewed as a module over
![]() $\Lambda _F$
. We fix a strongly admissible pro-p, uniform, p-adic Lie extension
$\Lambda _F$
. We fix a strongly admissible pro-p, uniform, p-adic Lie extension
![]() $F_\infty /F$
and let
$F_\infty /F$
and let
![]() $\operatorname {Sel}_{p^\infty }(E/F_\infty )$
be the Selmer group of E over
$\operatorname {Sel}_{p^\infty }(E/F_\infty )$
be the Selmer group of E over
![]() $F_\infty $
(see [Reference Lim21] for the definition). Throughout, we make the following assumption.
$F_\infty $
(see [Reference Lim21] for the definition). Throughout, we make the following assumption.
Assumption 2.3 With notation as above, assume that
![]() $\operatorname {Sel}_{p^\infty }(E/F_\infty )$
satisfies the
$\operatorname {Sel}_{p^\infty }(E/F_\infty )$
satisfies the
![]() $\mathfrak {M}_H(G)$
-conjecture. In greater detail, set
$\mathfrak {M}_H(G)$
-conjecture. In greater detail, set
![]() $X(E/F_\infty )$
to be the Pontryagin dual of
$X(E/F_\infty )$
to be the Pontryagin dual of
![]() $\operatorname {Sel}_{p^\infty }(E/F_\infty )$
. We assume that
$\operatorname {Sel}_{p^\infty }(E/F_\infty )$
. We assume that
 $$ \begin{align*}X_f(E/F_\infty):=\frac{X(E/F_\infty)}{X(E/F_\infty)[p^\infty]}\end{align*} $$
$$ \begin{align*}X_f(E/F_\infty):=\frac{X(E/F_\infty)}{X(E/F_\infty)[p^\infty]}\end{align*} $$
is finitely generated as a
![]() $\Lambda (H)$
-module.
$\Lambda (H)$
-module.
2.3 An analogue of Kida’s formula
Hachimori and Matsuno in [Reference Hachimori and Matsuno11] proved an analogue of Kida’s formula for Selmer groups of elliptic curves. We recall this result and a refinement due to Lim. Let F be a number field and
![]() $E_{/F}$
an elliptic curve. Let
$E_{/F}$
an elliptic curve. Let
![]() $L/F$
be a finite Galois extension such that
$L/F$
be a finite Galois extension such that
![]() $\operatorname {Gal}(L/F)$
is a p-group. Let
$\operatorname {Gal}(L/F)$
is a p-group. Let
![]() $P_1(E, L_{\operatorname {cyc}})$
(resp.
$P_1(E, L_{\operatorname {cyc}})$
(resp.
![]() $P_2(E, L_{\operatorname {cyc}})$
) be the set of primes
$P_2(E, L_{\operatorname {cyc}})$
) be the set of primes
![]() $\eta \nmid p$
of
$\eta \nmid p$
of
![]() $L_{\operatorname {cyc}}$
that are ramified in the extension
$L_{\operatorname {cyc}}$
that are ramified in the extension
![]() $L_{\operatorname {cyc}}/K_{\operatorname {cyc}}$
, at which E has split multiplicative reduction (resp. E has good reduction and
$L_{\operatorname {cyc}}/K_{\operatorname {cyc}}$
, at which E has split multiplicative reduction (resp. E has good reduction and
![]() $E(L_{\operatorname {cyc},\eta })[p]\neq 0$
). Given a prime
$E(L_{\operatorname {cyc},\eta })[p]\neq 0$
). Given a prime
![]() $\eta $
of
$\eta $
of
![]() $L_{\operatorname {cyc}}$
, set
$L_{\operatorname {cyc}}$
, set
![]() $e_{L_{\operatorname {cyc}}/K_{\operatorname {cyc}}}(\eta )$
to denote the ramification index of
$e_{L_{\operatorname {cyc}}/K_{\operatorname {cyc}}}(\eta )$
to denote the ramification index of
![]() $\eta $
with respect to the extension
$\eta $
with respect to the extension
![]() $L_{\operatorname {cyc}}/K_{\operatorname {cyc}}$
.
$L_{\operatorname {cyc}}/K_{\operatorname {cyc}}$
.
Theorem 2.4 (Lim)
Let
![]() $p\geq 5$
be a prime number, F a number field and
$p\geq 5$
be a prime number, F a number field and
![]() $E_{/F}$
an elliptic curve with good ordinary reduction at all primes of F above p. Let
$E_{/F}$
an elliptic curve with good ordinary reduction at all primes of F above p. Let
![]() $L/F$
be a Galois extension for which
$L/F$
be a Galois extension for which
![]() $\operatorname {Gal}(L/F)$
is a p-group. Assume that there is a pro-p strongly admissible p-adic Lie extension
$\operatorname {Gal}(L/F)$
is a p-group. Assume that there is a pro-p strongly admissible p-adic Lie extension
![]() $F_\infty /F$
such that
$F_\infty /F$
such that
-
(1)
 $F_\infty $
contains L.
$F_\infty $
contains L. -
(2) Assumption 2.3 is satisfied.
Then, the following assertions hold
-
(1)
 $\operatorname {Sel}_{p^\infty }(E/L_{\operatorname {cyc}})$
is cotorsion over the Iwasawa algebra
$\operatorname {Sel}_{p^\infty }(E/L_{\operatorname {cyc}})$
is cotorsion over the Iwasawa algebra
 $\Lambda _L$
,
$\Lambda _L$
, -
(2)
 $\mu _p(E/L)=[L:K]\mu _p(E/K)$
, and
$\mu _p(E/L)=[L:K]\mu _p(E/K)$
, and -
(3)
 $$ \begin{align*}\lambda_p(E/L)\,{=}\,&[L_{\operatorname{cyc}}:K_{\operatorname{cyc}}]\lambda_p(E/K)+\sum_{\eta\in P_1(E/L_{\operatorname{cyc}})} \left(e_{L_{\operatorname{cyc}}/K_{\operatorname{cyc}}}(\eta)-1\right)\\&+2\sum_{\eta\in P_2(E/L_{\operatorname{cyc}})} \left(e_{L_{\operatorname{cyc}}/K_{\operatorname{cyc}}}(\eta)-1\right).\end{align*} $$
$$ \begin{align*}\lambda_p(E/L)\,{=}\,&[L_{\operatorname{cyc}}:K_{\operatorname{cyc}}]\lambda_p(E/K)+\sum_{\eta\in P_1(E/L_{\operatorname{cyc}})} \left(e_{L_{\operatorname{cyc}}/K_{\operatorname{cyc}}}(\eta)-1\right)\\&+2\sum_{\eta\in P_2(E/L_{\operatorname{cyc}})} \left(e_{L_{\operatorname{cyc}}/K_{\operatorname{cyc}}}(\eta)-1\right).\end{align*} $$
Proof The result as stated follows from the results in [Reference Lim21], as we now explain. Note that since it is assumed that the Selmer group of E over
![]() $F_\infty $
satisfies the
$F_\infty $
satisfies the
![]() $\mathfrak {M}_H(G)$
-conjecture, it follows from [Reference Coates and Sujatha2, Proposition 2.5] that
$\mathfrak {M}_H(G)$
-conjecture, it follows from [Reference Coates and Sujatha2, Proposition 2.5] that
![]() $\operatorname {Sel}_{p^\infty }(E/L_{\operatorname {cyc}})$
is cotorsion over
$\operatorname {Sel}_{p^\infty }(E/L_{\operatorname {cyc}})$
is cotorsion over
![]() $\Lambda _L$
. First, we reduce to the case when
$\Lambda _L$
. First, we reduce to the case when
![]() $K_{\operatorname {cyc}}\cap L=K$
, i.e.,
$K_{\operatorname {cyc}}\cap L=K$
, i.e.,
![]() $[L:K]=[L_{\operatorname {cyc}}:K_{\operatorname {cyc}}]$
. Letting
$[L:K]=[L_{\operatorname {cyc}}:K_{\operatorname {cyc}}]$
. Letting
![]() $K'=K_{\operatorname {cyc}}\cap L$
, it is easy to see that if the result holds for the extensions
$K'=K_{\operatorname {cyc}}\cap L$
, it is easy to see that if the result holds for the extensions
![]() $L/K'$
and
$L/K'$
and
![]() $K'/K$
, then it holds for
$K'/K$
, then it holds for
![]() $L/K$
.
$L/K$
.
First, we prove that the result holds for
![]() $K'/K$
. It is a simple exercise to show that
$K'/K$
. It is a simple exercise to show that
![]() $\mu _p(E/K')=[K':K] \mu _p(E/K)$
. Furthermore
$\mu _p(E/K')=[K':K] \mu _p(E/K)$
. Furthermore
![]() $\lambda _p(E/K')$
is the
$\lambda _p(E/K')$
is the
![]() $\mathbb {Z}_p$
-corank of
$\mathbb {Z}_p$
-corank of
 $\operatorname {Sel}_{p^\infty }(E/K^{\prime }_{\operatorname {cyc}})$
. Since
$\operatorname {Sel}_{p^\infty }(E/K^{\prime }_{\operatorname {cyc}})$
. Since
![]() $K'$
is contained in
$K'$
is contained in
![]() $K_{\operatorname {cyc}}$
, we have that
$K_{\operatorname {cyc}}$
, we have that
 $K^{\prime }_{\operatorname {cyc}}=K_{\operatorname {cyc}}$
. Therefore,
$K^{\prime }_{\operatorname {cyc}}=K_{\operatorname {cyc}}$
. Therefore,
![]() $\lambda _p(E/K')$
is equal to
$\lambda _p(E/K')$
is equal to
![]() $\lambda _p(E/K)$
. Thus, the result is shown to hold for
$\lambda _p(E/K)$
. Thus, the result is shown to hold for
![]() $K'/K$
and it suffices to prove the result for
$K'/K$
and it suffices to prove the result for
![]() $L/K'$
. Upon replacing K with
$L/K'$
. Upon replacing K with
![]() $K'$
, we thus reduce to the case when
$K'$
, we thus reduce to the case when
![]() $[L:K]=[L_{\operatorname {cyc}}:K_{\operatorname {cyc}}]$
. In this setting, the result follows from [Reference Lim21, Theorem 4.1 and Section 5]. Indeed the decomposition conditions in loc. cit. are equivalent to the conditions on
$[L:K]=[L_{\operatorname {cyc}}:K_{\operatorname {cyc}}]$
. In this setting, the result follows from [Reference Lim21, Theorem 4.1 and Section 5]. Indeed the decomposition conditions in loc. cit. are equivalent to the conditions on
![]() $P_1$
and
$P_1$
and
![]() $P_2$
.▪
$P_2$
.▪
Remark 2.5 It should be noted here that in Section 5 of [Reference Lim21] an additional assumption is made, namely that F contains the pth roots of unity. This assumption is in place to guarantee the existence of an admissible p-adic Lie extension of L, see Lemma 4.2 of loc. cit. Since we have assumed that such an admissible p-adic Lie extension
![]() $F_\infty /L$
exists to begin with, there is no need for this additional assumption.
$F_\infty /L$
exists to begin with, there is no need for this additional assumption.
2.4 Main result
Let E be an elliptic curve over a number field F with good ordinary reduction at all primes above p. Throughout, we shall make the following assumption.
We introduce some further notation. Let
![]() $Q_1=Q_1(E,F_\infty )$
(resp.
$Q_1=Q_1(E,F_\infty )$
(resp.
![]() $Q_2=Q_2(E,F_\infty )$
) be the set of primes
$Q_2=Q_2(E,F_\infty )$
) be the set of primes
![]() $w\nmid p$
of
$w\nmid p$
of
![]() $F_{\operatorname {cyc}}$
that are ramified in
$F_{\operatorname {cyc}}$
that are ramified in
![]() $F_\infty $
, at which E has split multiplicative reduction (resp. E has good reduction and
$F_\infty $
, at which E has split multiplicative reduction (resp. E has good reduction and
![]() $E(F_{\operatorname {cyc},w})[p]\neq 0$
). We stress here that
$E(F_{\operatorname {cyc},w})[p]\neq 0$
). We stress here that
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
consist of subsets of primes of
$Q_2$
consist of subsets of primes of
![]() $F_{\operatorname {cyc}}$
and not
$F_{\operatorname {cyc}}$
and not
![]() $F_\infty $
. Recall that it is stipulated that only finitely many primes ramify in
$F_\infty $
. Recall that it is stipulated that only finitely many primes ramify in
![]() $F_\infty $
, and since all primes are finitely decomposed in
$F_\infty $
, and since all primes are finitely decomposed in
![]() $F_{\operatorname {cyc}}$
, it follows that
$F_{\operatorname {cyc}}$
, it follows that
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
are finite. For
$Q_2$
are finite. For
![]() $i=1,2$
, we set
$i=1,2$
, we set
![]() $q_i:=\#Q_i$
.
$q_i:=\#Q_i$
.
Theorem 2.6 Let n be a positive integer. Suppose that the conditions of Assumption 2.3 hold, then,
 $\operatorname {Sel}_{p^\infty }(E/F^{(n)}_{\operatorname {cyc}})$
is a cotorsion
$\operatorname {Sel}_{p^\infty }(E/F^{(n)}_{\operatorname {cyc}})$
is a cotorsion
![]() $\Lambda _{F^{(n)}}$
-module, with
$\Lambda _{F^{(n)}}$
-module, with
 $$ \begin{align*}\mu_p(E/F^{(n)})=p^{nd}\mu_p(E/F).\end{align*} $$
$$ \begin{align*}\mu_p(E/F^{(n)})=p^{nd}\mu_p(E/F).\end{align*} $$
Furthermore, we have that
 $$ \begin{align*}p^{n(d-1)}\lambda_p(E/F)\leq \lambda_p(E/F^{(n)})\leq p^{n(d-1)}\lambda_p(E/F)+\left(p^{n(d-1)}-p^{n(d-2)}\right)(q_1+2q_2).\end{align*} $$
$$ \begin{align*}p^{n(d-1)}\lambda_p(E/F)\leq \lambda_p(E/F^{(n)})\leq p^{n(d-1)}\lambda_p(E/F)+\left(p^{n(d-1)}-p^{n(d-2)}\right)(q_1+2q_2).\end{align*} $$
Proof According to Theorem 2.4,
 $\operatorname {Sel}_{p^\infty }(E/F^{(n)}_{\operatorname {cyc}})$
is a cotorsion module over
$\operatorname {Sel}_{p^\infty }(E/F^{(n)}_{\operatorname {cyc}})$
is a cotorsion module over
![]() $\Lambda _{F^{(n)}}$
and the
$\Lambda _{F^{(n)}}$
and the
![]() $\mu $
-invariant is given by
$\mu $
-invariant is given by
 $$ \begin{align*}\mu_p(E/F^{(n)})=[F^{(n)}:F]\mu_p(E/F)=p^{nd}\mu_p(E/F).\end{align*} $$
$$ \begin{align*}\mu_p(E/F^{(n)})=[F^{(n)}:F]\mu_p(E/F)=p^{nd}\mu_p(E/F).\end{align*} $$
Furthermore, the
![]() $\lambda $
-invariant is
$\lambda $
-invariant is
 $$ \begin{align*}\lambda_p(E/F^{(n)})=[F^{(n)}_{\operatorname{cyc}}:F_{\operatorname{cyc}}]\lambda_p(E/F)+\sum_{w\in P_1} \left(e(w)-1\right)+2\sum_{w\in P_2} \left(e(w)-1\right),\end{align*} $$
$$ \begin{align*}\lambda_p(E/F^{(n)})=[F^{(n)}_{\operatorname{cyc}}:F_{\operatorname{cyc}}]\lambda_p(E/F)+\sum_{w\in P_1} \left(e(w)-1\right)+2\sum_{w\in P_2} \left(e(w)-1\right),\end{align*} $$
where
![]() $e(w)$
is the ramification index of w in
$e(w)$
is the ramification index of w in
 $F^{(n)}_{\operatorname {cyc}}/F_{\operatorname {cyc}}$
,
$F^{(n)}_{\operatorname {cyc}}/F_{\operatorname {cyc}}$
,
![]() $P_1$
and
$P_1$
and
![]() $P_2$
are the set of primes of
$P_2$
are the set of primes of
 $F^{(n)}_{\operatorname {cyc}}$
defined as follows:
$F^{(n)}_{\operatorname {cyc}}$
defined as follows:
 $$ \begin{align*} & P_1=\{w\mid w\nmid p, E\text{ has split multiplicative reduction at }w\},\\ & P_2=\{w\mid w\nmid p, E\text{ has good reduction at }w\text{ and }E(\mathcal{F}_{n,w})\text{ has a point of order }p\}. \end{align*} $$
$$ \begin{align*} & P_1=\{w\mid w\nmid p, E\text{ has split multiplicative reduction at }w\},\\ & P_2=\{w\mid w\nmid p, E\text{ has good reduction at }w\text{ and }E(\mathcal{F}_{n,w})\text{ has a point of order }p\}. \end{align*} $$
Since p is odd, the primes
![]() $P_i$
lie above
$P_i$
lie above
![]() $Q_i$
, therefore,
$Q_i$
, therefore,
 $$ \begin{align*}\sum_{w\in P_i} \left(e(w)-1\right)=\sum_{v\in Q_i} \left(\sum_{w\mid v} \left(e(w)-1\right)\right).\end{align*} $$
$$ \begin{align*}\sum_{w\in P_i} \left(e(w)-1\right)=\sum_{v\in Q_i} \left(\sum_{w\mid v} \left(e(w)-1\right)\right).\end{align*} $$
Choose a prime
![]() $w_0\in P_i$
above v. Since
$w_0\in P_i$
above v. Since
![]() $e(w)$
is the same for all primes
$e(w)$
is the same for all primes
![]() $w|v$
, we have that
$w|v$
, we have that
 $$ \begin{align*}\sum_{w\mid v} \left(e(w)-1\right)=\left(1-e(w_0)^{-1}\right)\sum_{w\mid v}e(w)\leq \left(1-e(w_0)^{-1}\right)[F^{(n)}_{\operatorname{cyc}}:F_{\operatorname{cyc}}].\end{align*} $$
$$ \begin{align*}\sum_{w\mid v} \left(e(w)-1\right)=\left(1-e(w_0)^{-1}\right)\sum_{w\mid v}e(w)\leq \left(1-e(w_0)^{-1}\right)[F^{(n)}_{\operatorname{cyc}}:F_{\operatorname{cyc}}].\end{align*} $$
According to Lemma 2.2, H is uniform with
![]() $d-1$
generators. Note that
$d-1$
generators. Note that
 $[F^{(n)}_{\operatorname {cyc}}:F_{\operatorname {cyc}}]=[H:H_n]=p^{(d-1)n}$
. Since pro-p tame inertia is generated by a single element, it follows that
$[F^{(n)}_{\operatorname {cyc}}:F_{\operatorname {cyc}}]=[H:H_n]=p^{(d-1)n}$
. Since pro-p tame inertia is generated by a single element, it follows that
![]() $e(w_0)\leq p^{n}$
. Putting it all together, the result follows.▪
$e(w_0)\leq p^{n}$
. Putting it all together, the result follows.▪
Theorem 2.7 Let E be an elliptic curve defined over a number field F and
![]() $F_\infty $
a uniform pro-p extension of F satisfying aforementioned conditions and suppose that the Selmer group over
$F_\infty $
a uniform pro-p extension of F satisfying aforementioned conditions and suppose that the Selmer group over
![]() $F_{\operatorname {cyc}}$
is cotorsion as a
$F_{\operatorname {cyc}}$
is cotorsion as a
![]() -module. Then, we have the following bound
-module. Then, we have the following bound
 $$ \begin{align*}\operatorname{rank} E(F^{(n)})\leq p^{n(d-1)}\lambda_p(E/F)+\left(p^{n(d-1)}-p^{n(d-2)}\right)(q_1+2q_2).\end{align*} $$
$$ \begin{align*}\operatorname{rank} E(F^{(n)})\leq p^{n(d-1)}\lambda_p(E/F)+\left(p^{n(d-1)}-p^{n(d-2)}\right)(q_1+2q_2).\end{align*} $$
Proof The result immediately follows from Theorem 2.6 and the inequality
 $$ \begin{align*}\operatorname{rank} E(F^{(n)})\leq \lambda_p(E/F^{(n)}),\end{align*} $$
$$ \begin{align*}\operatorname{rank} E(F^{(n)})\leq \lambda_p(E/F^{(n)}),\end{align*} $$
see [Reference Greenberg10, Theorem 1.9].▪
Remark 2.8 The estimate above is stronger than [Reference Hung and Lim14, Theorem 3.1]. The error term is
![]() $O(p^{n(d-2)})$
and their method used relies on the work of Harris. In greater detail, [Reference Harris12, Theorem 1.10] is the key result used in the estimate in [Reference Hung and Lim14, Lemma 3.3]. Note however, that the error estimate of Hung–Lim is known to be 0 under certain additional constraints. Namely, if certain cohomology groups vanish and the p-torsion group
$O(p^{n(d-2)})$
and their method used relies on the work of Harris. In greater detail, [Reference Harris12, Theorem 1.10] is the key result used in the estimate in [Reference Hung and Lim14, Lemma 3.3]. Note however, that the error estimate of Hung–Lim is known to be 0 under certain additional constraints. Namely, if certain cohomology groups vanish and the p-torsion group
![]() $E(F_\infty )(p)$
is finite, see [Reference Hung and Lim14, Theorem 3.2] and the remark following it. If
$E(F_\infty )(p)$
is finite, see [Reference Hung and Lim14, Theorem 3.2] and the remark following it. If
![]() $F_\infty $
contains the extension
$F_\infty $
contains the extension
![]() $F(E[p^\infty ])$
generated by the p-primary torsion of E, then the error term of Hung–Lim is nonzero, even under additional assumptions. Also, even when the error term of Hung–Lim is 0, the the estimate above is strictly better when
$F(E[p^\infty ])$
generated by the p-primary torsion of E, then the error term of Hung–Lim is nonzero, even under additional assumptions. Also, even when the error term of Hung–Lim is 0, the the estimate above is strictly better when
![]() $q_1$
or
$q_1$
or
![]() $q_2$
is nonzero.
$q_2$
is nonzero.
The improvement in the bound has some nontrivial consequences, which we shall explain in the next section. The following is a Corollary to Theorem 2.6 and is entirely unconditional.
Corollary 2.9 Let E and
![]() $F_\infty $
be as in Theorem 2.7. Assume that
$F_\infty $
be as in Theorem 2.7. Assume that
![]() $q_1=q_2=0$
and
$q_1=q_2=0$
and
Then,
 $\operatorname {Sel}_{p^\infty }(E/F^{(n)}_{\operatorname {cyc}})=0$
for all n.
$\operatorname {Sel}_{p^\infty }(E/F^{(n)}_{\operatorname {cyc}})=0$
for all n.
Proof Since the
![]() $\mu $
-invariant
$\mu $
-invariant
![]() $\mu _p(E/F)=0$
, it follows that
$\mu _p(E/F)=0$
, it follows that
![]() $\mathfrak {M}_H(G)$
is satisfied for
$\mathfrak {M}_H(G)$
is satisfied for
![]() $F_\infty $
, see [Reference Coates and Sujatha2, Theorem 2.1]. By Theorem 2.6, it follows that the
$F_\infty $
, see [Reference Coates and Sujatha2, Theorem 2.1]. By Theorem 2.6, it follows that the
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
-invariants of
$\lambda $
-invariants of
 $\operatorname {Sel}_{p^\infty }(E/F^{(n)}_{\operatorname {cyc}})$
are
$\operatorname {Sel}_{p^\infty }(E/F^{(n)}_{\operatorname {cyc}})$
are
![]() $0$
, hence,
$0$
, hence,
 $\operatorname {Sel}_{p^\infty }(E/F^{(n)}_{\operatorname {cyc}})$
is finite. On the other hand, this Selmer does not contain any finite index submodules (see [Reference Greenberg9, Proposition 4.14]), hence, must be 0.▪
$\operatorname {Sel}_{p^\infty }(E/F^{(n)}_{\operatorname {cyc}})$
is finite. On the other hand, this Selmer does not contain any finite index submodules (see [Reference Greenberg9, Proposition 4.14]), hence, must be 0.▪
3 Special cases
In this section, we study special cases of Theorem 2.7. Assume throughout that the Assumption 2.3 is satisfied. Recall from the proof of Theorem 2.4 that this in particular implies that
![]() $\operatorname {Sel}_{p^\infty }(E/L)$
is cotorsion over
$\operatorname {Sel}_{p^\infty }(E/L)$
is cotorsion over
![]() $\Lambda _L$
for every number field extension
$\Lambda _L$
for every number field extension
![]() $L/K$
contained in
$L/K$
contained in
![]() $F_\infty $
.
$F_\infty $
.
3.1
 $\mathbb {Z}_p^d$
-extensions
$\mathbb {Z}_p^d$
-extensions
Throughout this subsection, F will be an abelian number field and
![]() $E_{/\mathbb {Q}}$
an elliptic curve with good ordinary reduction at p. Let
$E_{/\mathbb {Q}}$
an elliptic curve with good ordinary reduction at p. Let
![]() $F_\infty $
be the composite of all
$F_\infty $
be the composite of all
![]() $\mathbb {Z}_p$
-extensions of F, note that
$\mathbb {Z}_p$
-extensions of F, note that
 $G=\operatorname {Gal}(F_\infty /F)\simeq \mathbb {Z}_p^d$
, where
$G=\operatorname {Gal}(F_\infty /F)\simeq \mathbb {Z}_p^d$
, where
![]() $d=r_2(F)+1$
. For instance, when F is an imaginary quadratic field, then, this gives a
$d=r_2(F)+1$
. For instance, when F is an imaginary quadratic field, then, this gives a
![]() $\mathbb {Z}_p^2$
-extension of F. To emphasize the dependence on the prime p, we denote the extension by
$\mathbb {Z}_p^2$
-extension of F. To emphasize the dependence on the prime p, we denote the extension by
![]() $F_\infty (p)$
. On the other hand, it follows from results of Kato and Rohlrich [Reference Hachimori and Matsuno11, Theorem 2.2] that the Selmer group
$F_\infty (p)$
. On the other hand, it follows from results of Kato and Rohlrich [Reference Hachimori and Matsuno11, Theorem 2.2] that the Selmer group
![]() $\operatorname {Sel}_{p^\infty }(E/F_\infty )$
is cotorsion as a
$\operatorname {Sel}_{p^\infty }(E/F_\infty )$
is cotorsion as a
![]() -module. It is well known that any
-module. It is well known that any
![]() $\mathbb {Z}_p$
-extension is unramified away from p (see [Reference Washington27]), hence, the composite of such extensions has the same property. Let us state a few Corollaries to Theorem 2.7, the first of which gives a simple criterion for the rank to be zero throughout the
$\mathbb {Z}_p$
-extension is unramified away from p (see [Reference Washington27]), hence, the composite of such extensions has the same property. Let us state a few Corollaries to Theorem 2.7, the first of which gives a simple criterion for the rank to be zero throughout the
![]() $\mathbb {Z}_p^d$
-tower.
$\mathbb {Z}_p^d$
-tower.
Corollary 3.1 Let E be as above and assume that
![]() $\lambda _p(E/F_{\operatorname {cyc}})=0$
. Then,
$\lambda _p(E/F_{\operatorname {cyc}})=0$
. Then,
 $$ \begin{align*}\operatorname{rank} E(F^{(n)})=0\end{align*} $$
$$ \begin{align*}\operatorname{rank} E(F^{(n)})=0\end{align*} $$
for all
![]() $n\in \mathbb {Z}_{\geq 1}$
and
$n\in \mathbb {Z}_{\geq 1}$
and
 $$ \begin{align*}\mu_p(E/F^{(n)})=p^{nd}\mu_p(E/F).\end{align*} $$
$$ \begin{align*}\mu_p(E/F^{(n)})=p^{nd}\mu_p(E/F).\end{align*} $$
Proof Note that since E has good ordinary reduction at the primes above p and
the Mordell–Weil rank of E is 0. Since
![]() $F_\infty $
is unramified at all primes
$F_\infty $
is unramified at all primes
![]() $w\nmid p$
, the quantities
$w\nmid p$
, the quantities
![]() $q_1$
and
$q_1$
and
![]() $q_2$
in Theorem 2.7 are both equal to 0.▪
$q_2$
in Theorem 2.7 are both equal to 0.▪
Remark 3.2 When F is an imaginary quadratic field and E is a CM elliptic curve over F, the result of Hung–Lim in the above context shall imply that the rank in bounded in the tower, however, not identically 0. In the more general case, their result implies that the growth is
![]() $O(p^{n(d-2)})$
unless certain homology groups are known to vanish, see the discussion after [Reference Hung and Lim14, Theorem 3.2].
$O(p^{n(d-2)})$
unless certain homology groups are known to vanish, see the discussion after [Reference Hung and Lim14, Theorem 3.2].
Example: Picking an elliptic curve
![]() $E_{/\mathbb {Q}}$
at random, there are typically some primes at which
$E_{/\mathbb {Q}}$
at random, there are typically some primes at which
![]() $E[p]$
is residually reducible as a Galois module. At these primes, it is possible that the
$E[p]$
is residually reducible as a Galois module. At these primes, it is possible that the
![]() $\mu $
-invariant
$\mu $
-invariant
![]() $\mu _p(E/\mathbb {Q})$
does not vanish. For instance, let’s pick the elliptic curve of smallest conductor with cremona label 11a2. We find that E has good ordinary reduction at
$\mu _p(E/\mathbb {Q})$
does not vanish. For instance, let’s pick the elliptic curve of smallest conductor with cremona label 11a2. We find that E has good ordinary reduction at
![]() $5$
with
$5$
with
![]() $\mu _5(E/\mathbb {Q})=2$
and
$\mu _5(E/\mathbb {Q})=2$
and
![]() $\lambda _5(E/\mathbb {Q})=0$
. Suppose that there is an imaginary quadratic field
$\lambda _5(E/\mathbb {Q})=0$
. Suppose that there is an imaginary quadratic field
![]() $F/\mathbb {Q}$
in which
$F/\mathbb {Q}$
in which
![]() $\operatorname {rank} E(F)=0$
and
$\operatorname {rank} E(F)=0$
and
![]() $\lambda _5(E/F)=0$
as well. Let
$\lambda _5(E/F)=0$
as well. Let
![]() $F_\infty $
be the
$F_\infty $
be the
![]() $\mathbb {Z}_p^2$
-extension of F. Then, indeed, since
$\mathbb {Z}_p^2$
-extension of F. Then, indeed, since
![]() $\mu _5(E/F)\geq 2$
, the above result implies that
$\mu _5(E/F)\geq 2$
, the above result implies that
 $$ \begin{align*}\mu_5(E/F^{(n)})\geq 2p^{2n}\end{align*} $$
$$ \begin{align*}\mu_5(E/F^{(n)})\geq 2p^{2n}\end{align*} $$
for all
![]() $n\geq 1$
, however, the rank of
$n\geq 1$
, however, the rank of
![]() $E(F_n)$
remains
$E(F_n)$
remains
![]() $0$
throughout. Unfortunately, the author is not aware of any existing computer packages that can compute the
$0$
throughout. Unfortunately, the author is not aware of any existing computer packages that can compute the
![]() $\lambda $
-invariant over an imaginary quadratic field.
$\lambda $
-invariant over an imaginary quadratic field.
Corollary 3.3 Let
![]() $E_{/\mathbb {Q}}$
be an elliptic curve and F an abelian number field satisfying
$E_{/\mathbb {Q}}$
be an elliptic curve and F an abelian number field satisfying
-
(1)
 $\operatorname {rank} E(F)=0$
and
$\operatorname {rank} E(F)=0$
and -
(2) E does not have complex multiplication.
Then, for
![]() $100\%$
of primes p at which E has good ordinary reduction,
$100\%$
of primes p at which E has good ordinary reduction,
Proof In her thesis [Reference Kundu16, Theorem 5.1.1], Kundu generalized a result of Greenberg to show that the proportion of primes p such that
-
(1) E has good ordinary reduction at the primes of F above p and
-
(2)
 $\operatorname {Sel}_{p^\infty }(E/F_{\operatorname {cyc}})=0$
,
$\operatorname {Sel}_{p^\infty }(E/F_{\operatorname {cyc}})=0$
,
is
![]() $100\%$
. The result follows from this and Corollary 3.1.▪
$100\%$
. The result follows from this and Corollary 3.1.▪
The following is a special case of [Reference Hung and Lim14, Conjecture 1].
Conjecture 3.4 [Reference Hung and Lim14, Conjecture 1’]
Let E be an elliptic curve over an imaginary quadratic field F,
![]() $p\geq 5$
a prime and
$p\geq 5$
a prime and
![]() $F_\infty $
be the
$F_\infty $
be the
![]() $\mathbb {Z}_p^2$
-extension of F. Assume that the following conditions are satisfied:
$\mathbb {Z}_p^2$
-extension of F. Assume that the following conditions are satisfied:
-
(1) E has good ordinary reduction at all primes above p and
-
(2) Assumption 2.3 is satisfied.
Then, we have that
 $\operatorname {rank} E(F^{(n)})\leq \operatorname {rank} E(F_{\operatorname {cyc}}) p^{n}$
for all
$\operatorname {rank} E(F^{(n)})\leq \operatorname {rank} E(F_{\operatorname {cyc}}) p^{n}$
for all
![]() $n\geq 1$
.
$n\geq 1$
.
Corollary 3.5 Consider the setting of the above conjecture. Under Assumption 2.3, the Theorem 2.7 specializes to give that
 $$ \begin{align*}\operatorname{rank} E(F^{(n)})\leq \lambda_p(E/F) p^{n}.\end{align*} $$
$$ \begin{align*}\operatorname{rank} E(F^{(n)})\leq \lambda_p(E/F) p^{n}.\end{align*} $$
Thus, the Conjecture is true when
Remark 3.6 Note that
 $\lambda _p(E/F)\geq \operatorname {rank} E(F^{(n)})$
for all n and hence,
$\lambda _p(E/F)\geq \operatorname {rank} E(F^{(n)})$
for all n and hence,
![]() $\lambda _p(E/F)\geq \operatorname {rank} E(F_{\operatorname {cyc}})$
. Indeed, it can be expected that
$\lambda _p(E/F)\geq \operatorname {rank} E(F_{\operatorname {cyc}})$
. Indeed, it can be expected that
![]() $\lambda _p(E/F)=\operatorname {rank} E(F)$
for
$\lambda _p(E/F)=\operatorname {rank} E(F)$
for
![]() $100\%$
of primes above which E has good ordinary reduction. There is much evidence pointing towards this expectation for elliptic curves defined over the rationals, see [Reference Kundu and Ray18]. We do expect that similar arguments do carry over to elliptic curves over imaginary quadratic fields.
$100\%$
of primes above which E has good ordinary reduction. There is much evidence pointing towards this expectation for elliptic curves defined over the rationals, see [Reference Kundu and Ray18]. We do expect that similar arguments do carry over to elliptic curves over imaginary quadratic fields.
3.2 False-Tate curve extensions
Let
![]() $\ell $
be a finite set of prime numbers that are coprime to p and let
$\ell $
be a finite set of prime numbers that are coprime to p and let
![]() $F_\infty $
be the False-Tate curve extension of
$F_\infty $
be the False-Tate curve extension of
![]() $F=\mathbb {Q}(\mu _p)$
, given by
$F=\mathbb {Q}(\mu _p)$
, given by
 $$ \begin{align*}F_\infty:=\mathbb{Q}(\mu_{p^\infty},\ell^{\frac{1}{p^{\infty}}}).\end{align*} $$
$$ \begin{align*}F_\infty:=\mathbb{Q}(\mu_{p^\infty},\ell^{\frac{1}{p^{\infty}}}).\end{align*} $$
In other words, it is the extension obtained by adjoining all p-power roots of
![]() $1$
and
$1$
and
![]() $\ell $
. It is easy to see that
$\ell $
. It is easy to see that
![]() $F_\infty /F$
is a uniform pro-p extension of F of dimension
$F_\infty /F$
is a uniform pro-p extension of F of dimension
![]() $d=2$
. Thus Theorem 2.7 specializes to give us that
$d=2$
. Thus Theorem 2.7 specializes to give us that
 $$ \begin{align*}\operatorname{rank} E(F^{(n)})\leq \lambda_p(E/F)p^n+(p^n-1)\left(q_1+2q_2\right).\end{align*} $$
$$ \begin{align*}\operatorname{rank} E(F^{(n)})\leq \lambda_p(E/F)p^n+(p^n-1)\left(q_1+2q_2\right).\end{align*} $$
Let us compute the values of
![]() $q_1$
and
$q_1$
and
![]() $q_2$
for a given example. We note that it is difficult to compute
$q_2$
for a given example. We note that it is difficult to compute
![]() $\lambda _p(E/F)$
due to the base change to
$\lambda _p(E/F)$
due to the base change to
![]() $F=\mathbb {Q}(\mu _p)$
.
$F=\mathbb {Q}(\mu _p)$
.
Example: We pick an elliptic curve and prime at random. Let
![]() $E=$
11a2 in Cremona label and
$E=$
11a2 in Cremona label and
![]() $p=7$
. The elliptic curve is defined over
$p=7$
. The elliptic curve is defined over
![]() $\mathbb {Q}$
and we consider its base change to
$\mathbb {Q}$
and we consider its base change to
![]() $F=\mathbb {Q}(\mu _7)$
. It follows from Assumption 2.3 and from the proof of Theorem 2.4 that
$F=\mathbb {Q}(\mu _7)$
. It follows from Assumption 2.3 and from the proof of Theorem 2.4 that
![]() $\operatorname {Sel}_{7^\infty }(E/\mathbb {Q}(\mu _{7^\infty }))$
is cotorsion over
$\operatorname {Sel}_{7^\infty }(E/\mathbb {Q}(\mu _{7^\infty }))$
is cotorsion over
![]() $\Lambda _F$
. Note that since F is an abelian extension of
$\Lambda _F$
. Note that since F is an abelian extension of
![]() $\mathbb {Q}$
, the cotorsion property of the Selmer group (over
$\mathbb {Q}$
, the cotorsion property of the Selmer group (over
![]() $\Lambda _F$
) also follows from results due to Kato, see [Reference Kato15]. The image of the residual representation at
$\Lambda _F$
) also follows from results due to Kato, see [Reference Kato15]. The image of the residual representation at
![]() $p=7$
contains
$p=7$
contains
![]() $\operatorname {SL}_2(\mathbb {F}_7)$
, as stated in the link provided. Hence, after base change to
$\operatorname {SL}_2(\mathbb {F}_7)$
, as stated in the link provided. Hence, after base change to
![]() $\mathbb {Q}(\mu _7)$
the image of the residual representation will still contain
$\mathbb {Q}(\mu _7)$
the image of the residual representation will still contain
![]() $\operatorname {SL}_2(\mathbb {F}_7)$
. It is thus reasonable to expect that the
$\operatorname {SL}_2(\mathbb {F}_7)$
. It is thus reasonable to expect that the
![]() $\mu $
-invariant
$\mu $
-invariant
![]() $\mu _7(E/F)=0$
, however, this is difficult to prove and needs to be assumed. Consider the False Tate extension
$\mu _7(E/F)=0$
, however, this is difficult to prove and needs to be assumed. Consider the False Tate extension
 $$ \begin{align*}F_\infty:=\mathbb{Q}(\mu_{7^\infty},11^{\frac{1}{7^{\infty}}}).\end{align*} $$
$$ \begin{align*}F_\infty:=\mathbb{Q}(\mu_{7^\infty},11^{\frac{1}{7^{\infty}}}).\end{align*} $$
Then, E has split multiplicative reduction at
![]() $11$
, hence
$11$
, hence
![]() $q_2=0$
, however,
$q_2=0$
, however,
![]() $q_1>0$
. Since
$q_1>0$
. Since
![]() $11^3\equiv 1\mod {7}$
and
$11^3\equiv 1\mod {7}$
and
![]() $11^3\not \equiv 1\mod {49}$
, there are precisely two primes above
$11^3\not \equiv 1\mod {49}$
, there are precisely two primes above
![]() $11$
in
$11$
in
![]() $F_{\operatorname {cyc}}=\mathbb {Q}(\mu _{7^\infty })$
. It follows that
$F_{\operatorname {cyc}}=\mathbb {Q}(\mu _{7^\infty })$
. It follows that
![]() $q_1=2$
. Putting it all together, we find that
$q_1=2$
. Putting it all together, we find that
 $$ \begin{align*}\operatorname{rank} E(F^{(n)})\leq \lambda_7(E/F)7^n+2(7^n-1).\end{align*} $$
$$ \begin{align*}\operatorname{rank} E(F^{(n)})\leq \lambda_7(E/F)7^n+2(7^n-1).\end{align*} $$
Next, we prove a statistical result.
Corollary 3.7 Consider the elliptic curve
![]() $E=11a2$
from the example above and set
$E=11a2$
from the example above and set
![]() $p=7$
. There is a positive density set of primes
$p=7$
. There is a positive density set of primes
![]() $\ell $
such that
$\ell $
such that
 $$ \begin{align*}\operatorname{rank}E\left(\mathbb{Q}(\mu_{7^{n+1}}, \ell^{\frac{1}{7^n}})\right)\leq \lambda_7(E/F)7^n\end{align*} $$
$$ \begin{align*}\operatorname{rank}E\left(\mathbb{Q}(\mu_{7^{n+1}}, \ell^{\frac{1}{7^n}})\right)\leq \lambda_7(E/F)7^n\end{align*} $$
for any integer
![]() $n\geq 1$
.
$n\geq 1$
.
Proof For each prime number
![]() $\ell $
such that
$\ell $
such that
![]() $\ell \equiv 1\mod {7}$
, let
$\ell \equiv 1\mod {7}$
, let
![]() $F_\infty ^{(\ell )}$
denote the extension
$F_\infty ^{(\ell )}$
denote the extension
 $\mathbb {Q}(\mu _{7^\infty }, \ell ^{\frac {1}{7^\infty }})$
. Note that
$\mathbb {Q}(\mu _{7^\infty }, \ell ^{\frac {1}{7^\infty }})$
. Note that
![]() $\ell $
splits in
$\ell $
splits in
![]() $\mathbb {Q}(\mu _7)$
and the only prime other than
$\mathbb {Q}(\mu _7)$
and the only prime other than
![]() $7$
that ramifies in
$7$
that ramifies in
![]() $F_\infty ^{(\ell )}$
is
$F_\infty ^{(\ell )}$
is
![]() $\ell $
. Since E has bad reduction at only finitely many primes, we deduce that
$\ell $
. Since E has bad reduction at only finitely many primes, we deduce that
![]() $q_1=0$
for all extensions
$q_1=0$
for all extensions
![]() $F_\infty ^{(\ell )}$
except for finitely many choices of
$F_\infty ^{(\ell )}$
except for finitely many choices of
![]() $\ell $
. Recall that
$\ell $
. Recall that
![]() $Q_2$
consists of the primes
$Q_2$
consists of the primes
![]() $w\nmid 7$
of
$w\nmid 7$
of
![]() $F_{\operatorname {cyc}}$
that are ramified in
$F_{\operatorname {cyc}}$
that are ramified in
![]() $F_\infty $
, such that E has good reduction at w and
$F_\infty $
, such that E has good reduction at w and
![]() $E(F_{\operatorname {cyc},w})[7]\neq 0$
. Since the formal group of E at w is pro-
$E(F_{\operatorname {cyc},w})[7]\neq 0$
. Since the formal group of E at w is pro-
![]() $\ell $
,
$\ell $
,
![]() $E(F_{\operatorname {cyc},w})[7]\simeq E(k_w)[7]$
, where
$E(F_{\operatorname {cyc},w})[7]\simeq E(k_w)[7]$
, where
![]() $k_w$
is the residue field of
$k_w$
is the residue field of
![]() $F_{\operatorname {cyc},w}$
. Since
$F_{\operatorname {cyc},w}$
. Since
![]() $k_w$
is a
$k_w$
is a
![]() $7$
-extension of
$7$
-extension of
![]() $\mathbb {F}_\ell $
, it follows that
$\mathbb {F}_\ell $
, it follows that
![]() $E(k_w)[7]\neq 0$
if and only if
$E(k_w)[7]\neq 0$
if and only if
![]() $E(\mathbb {F}_\ell )[7]\neq 0$
. Thus, the prime w lies in
$E(\mathbb {F}_\ell )[7]\neq 0$
. Thus, the prime w lies in
![]() $Q_2$
if the following conditions are satisfied:
$Q_2$
if the following conditions are satisfied:
-
(1)
 $w|\ell $
,
$w|\ell $
, -
(2) E has good reduction at
 $\ell $
, and
$\ell $
, and -
(3)
 $E(\mathbb {F}_\ell )[7]\neq 0$
.
$E(\mathbb {F}_\ell )[7]\neq 0$
.
This latter condition is satisfied for
![]() $\frac {1}{7}$
of all primes
$\frac {1}{7}$
of all primes
![]() $\ell $
, see [Reference Cojocaru3, Section 2] for further details. We show that a similar application of the Chebotarev density theorem shows that for a positive proportion of the primes
$\ell $
, see [Reference Cojocaru3, Section 2] for further details. We show that a similar application of the Chebotarev density theorem shows that for a positive proportion of the primes
![]() $\ell $
, both
$\ell $
, both
![]() $q_1$
and
$q_1$
and
![]() $q_2$
are
$q_2$
are
![]() $0$
. Note that if a prime
$0$
. Note that if a prime
![]() $\ell $
splits in
$\ell $
splits in
![]() $\mathbb {Q}(\mu _7)$
precisely when
$\mathbb {Q}(\mu _7)$
precisely when
![]() $\ell \equiv 1\mod {7}$
. Let
$\ell \equiv 1\mod {7}$
. Let
![]() $\bar {\rho }:\operatorname {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})\rightarrow \operatorname {GL}_2(\mathbb {F}_7)$
be the Galois representation on the
$\bar {\rho }:\operatorname {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})\rightarrow \operatorname {GL}_2(\mathbb {F}_7)$
be the Galois representation on the
![]() $7$
-torsion points
$7$
-torsion points
![]() $E[7]$
. Denote by
$E[7]$
. Denote by
![]() $\mathbb {Q}(\bar {\rho })$
the number field fixed by the kernel of
$\mathbb {Q}(\bar {\rho })$
the number field fixed by the kernel of
![]() $\bar {\rho }$
. Note that
$\bar {\rho }$
. Note that
![]() $\operatorname {det}\bar {\rho }$
is the mod-
$\operatorname {det}\bar {\rho }$
is the mod-
![]() $7$
cyclotomic character, which we denote by
$7$
cyclotomic character, which we denote by
![]() $\bar {\chi }$
. Therefore, the field
$\bar {\chi }$
. Therefore, the field
![]() $\mathbb {Q}(\bar {\rho })$
contains
$\mathbb {Q}(\bar {\rho })$
contains
![]() $\mathbb {Q}(\mu _7)$
, which is the field fixed by the kernel of
$\mathbb {Q}(\mu _7)$
, which is the field fixed by the kernel of
![]() $\bar {\chi }$
. Let
$\bar {\chi }$
. Let
![]() $\ell \neq 7$
be a prime at which E has good reduction, note that
$\ell \neq 7$
be a prime at which E has good reduction, note that
![]() $\bar {\rho }$
is unramified at
$\bar {\rho }$
is unramified at
![]() $\ell $
. Let
$\ell $
. Let
![]() $\sigma _\ell \in \operatorname {Gal}\left (\mathbb {Q}(\bar {\rho })/\mathbb {Q}\right )$
denote the Frobenius element at
$\sigma _\ell \in \operatorname {Gal}\left (\mathbb {Q}(\bar {\rho })/\mathbb {Q}\right )$
denote the Frobenius element at
![]() $\ell $
, it is well known that the characteristic polynomial of
$\ell $
, it is well known that the characteristic polynomial of
![]() $\bar {\rho }(\sigma _\ell )$
is given by
$\bar {\rho }(\sigma _\ell )$
is given by
Thus, if
![]() $\ell $
is a prime such that
$\ell $
is a prime such that
then,
![]() $\ell $
splits in
$\ell $
splits in
![]() $\mathbb {Q}(\mu _7)$
and
$\mathbb {Q}(\mu _7)$
and
![]() $E(\mathbb {F}_\ell )[7]= 0$
. We show that there is a positive density set of primes
$E(\mathbb {F}_\ell )[7]= 0$
. We show that there is a positive density set of primes
![]() $\ell $
satisfying the above conditions (3.1). According to the LMFDB Database [Reference Cremona, Jones, Sutherland and Voight5], the image of
$\ell $
satisfying the above conditions (3.1). According to the LMFDB Database [Reference Cremona, Jones, Sutherland and Voight5], the image of
![]() $\bar {\rho }$
contains
$\bar {\rho }$
contains
![]() $\operatorname {SL}_2(\mathbb {F}_7)$
. Thus there is
$\operatorname {SL}_2(\mathbb {F}_7)$
. Thus there is
![]() $\sigma \in \operatorname {Gal}(\mathbb {Q}(\bar {\rho })/\mathbb {Q})$
such that
$\sigma \in \operatorname {Gal}(\mathbb {Q}(\bar {\rho })/\mathbb {Q})$
such that
 $\bar {\rho }(\sigma )= \left ( {\begin {array}{cc} 2 & 1 \\ 1 & 1 \\ \end {array} } \right )$
, and thus satisfies (3.1). According to the Chebotarev density theorem, there is a positive proportion of primes such that
$\bar {\rho }(\sigma )= \left ( {\begin {array}{cc} 2 & 1 \\ 1 & 1 \\ \end {array} } \right )$
, and thus satisfies (3.1). According to the Chebotarev density theorem, there is a positive proportion of primes such that
![]() $\sigma _\ell =\sigma $
, and thus,
$\sigma _\ell =\sigma $
, and thus,
 $\bar {\rho }(\sigma _\ell )= \left ( {\begin {array}{cc} 2 & 1 \\ 1 & 1 \\ \end {array} } \right )$
. As a result, there is a positive density set of primes
$\bar {\rho }(\sigma _\ell )= \left ( {\begin {array}{cc} 2 & 1 \\ 1 & 1 \\ \end {array} } \right )$
. As a result, there is a positive density set of primes
![]() $\ell $
such that
$\ell $
such that
![]() $q_1$
and
$q_1$
and
![]() $q_2$
are both zero, and this completes the proof.▪
$q_2$
are both zero, and this completes the proof.▪
3.3 The field generated by torsion points
We come to the example in which
![]() $F_\infty $
is the field
$F_\infty $
is the field
![]() $\mathbb {Q}(E[p^\infty ])$
, i.e., the field generated by the p-primary torsion points of E. Assume that E does not have complex multiplication. Then, by Serre’s Open image theorem (see [Reference Serre25, Section 4 and Theorem 3]), G is a finite index subgroup of
$\mathbb {Q}(E[p^\infty ])$
, i.e., the field generated by the p-primary torsion points of E. Assume that E does not have complex multiplication. Then, by Serre’s Open image theorem (see [Reference Serre25, Section 4 and Theorem 3]), G is a finite index subgroup of
![]() $\operatorname {GL}_2(\mathbb {Z}_p)$
and it follows from this that the dimension of G is
$\operatorname {GL}_2(\mathbb {Z}_p)$
and it follows from this that the dimension of G is
![]() $4$
. In this setting,
$4$
. In this setting,
![]() $F=\mathbb {Q}(E[p])$
, and
$F=\mathbb {Q}(E[p])$
, and
![]() $F^{(n)}=\mathbb {Q}(E[p^{n+1}])$
. We find that
$F^{(n)}=\mathbb {Q}(E[p^{n+1}])$
. We find that
 $$ \begin{align*}\operatorname{rank} E(F_n)\leq \lambda_p(E/F)p^{3n}+q_1(p^{3n}-p^{2n}),\end{align*} $$
$$ \begin{align*}\operatorname{rank} E(F_n)\leq \lambda_p(E/F)p^{3n}+q_1(p^{3n}-p^{2n}),\end{align*} $$
where
![]() $q_1$
is simply the number of primes
$q_1$
is simply the number of primes
![]() $\ell \neq p$
at which E has split multiplicative reduction, and
$\ell \neq p$
at which E has split multiplicative reduction, and
![]() $q_2=0$
. On the other hand, according to [Reference Hung and Lim14, Remark after Theorem 3.2] the result of Hung–Lim [Reference Hung and Lim14, Theorem 3.2] gives
$q_2=0$
. On the other hand, according to [Reference Hung and Lim14, Remark after Theorem 3.2] the result of Hung–Lim [Reference Hung and Lim14, Theorem 3.2] gives
 $$ \begin{align*}\operatorname{rank} E(F_n)\leq (\lambda_p(E/F)+q_1)p^{3n}+8, \end{align*} $$
$$ \begin{align*}\operatorname{rank} E(F_n)\leq (\lambda_p(E/F)+q_1)p^{3n}+8, \end{align*} $$
when the whole dual Selmer group
![]() $\mathscr {X}(E/F_\infty )$
is finitely generated over
$\mathscr {X}(E/F_\infty )$
is finitely generated over
![]() $\Lambda (H)$
.
$\Lambda (H)$
.
Acknowledgment
The author is grateful to Debanjana Kundu for pointing out an inaccuracy in the previous draft. The author also thank the anonymous referee for a timely and thorough reading of the manuscript and for suggestion various pertinent corrections.