Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T15:08:15.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic first boundary value problem for holomorphic functions of several complex variables

Part of: Holomorphic convexity Miscellaneous topics of analysis in the complex domain Holomorphic functions of several complex variables

Published online by Cambridge University Press:  18 May 2021

Paul M. Gauthier  and
Mohammad Shirazi Open the ORCID record for Mohammad Shirazi [Opens in a new window]
Paul M. Gauthier*
Affiliation:
Département de mathématiques et de statistique, Université de Montréal, Montréal, QCH3C 3J7, Canada
Mohammad Shirazi
Affiliation:
Department of Mathematics and Statistics, McGill University, Montréal, QCH3A 0B9, Canada e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1955, Lehto showed that, for every measurable function 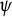$\psi $ on the unit circle 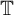${\mathbb T}$ , there is a function f holomorphic in the unit disc 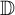${{\mathbb D}}$ , having 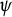$\psi $ as radial limit a.e. on 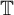${\mathbb T}$ . We consider an analogous boundary value problem, where the unit disc is replaced by a Stein domain on a complex manifold and radial approach to a boundary point p is replaced by (asymptotically) total approach to p.

Keywords

Boundary valuesholomorphic functionscomplex approximation

MSC classification

Primary: 30E25: Boundary value problems
Secondary: 32A40: Boundary behavior of holomorphic functions 30E10: Approximation in the complex domain 32E30: Holomorphic and polynomial approximation, Runge pairs, interpolation
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 2 , June 2022 , pp. 361 - 380
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The present research was supported by NSERC (Canada) grant RGPIN-2016-04107.

References

Alexander, H. and Wermer, J., Several complex variables and Banach algebras. 3rd ed., Graduate Texts in Mathematics, 35, Springer, New York, 1998.Google Scholar
Anderson, B. D. O. and Vongpanitlerdm, S., Network analysis and synthesis: a modern systems theory approach. Prentice Hall, Englewood Cliffs, NJ, 1973.Google Scholar
Bayart, F. and Gauthier, P. M., Functions universal for all translation operators in several complex variables. Canad. Math. Bull. 60(2017), no. 3, 462–469.CrossRefGoogle Scholar
Falcó, J. and Gauthier, P. M., An asymptotic holomorphic boundary problem on arbitrary open sets in Riemann surfaces. J. Approx. Theory 257(2020), 105451.CrossRefGoogle Scholar
Falcó, J. and Gauthier, P. M., Approximation in measure: Dirichlet problem, universality and the Riemann hypothesis. Izv. Ross. Akad. Nauk Ser. Mat. 85(2021), no. 3, 222–238. Izv. Math. 85, no. 3, 1–15.Google Scholar
Falcó, J. and Gauthier, P. M., Asymptotic first boundary problem for elliptic operators. Submitted, 2021.CrossRefGoogle Scholar
Izzo, A. J., Polynomial hulls of arcs and curves. Proc. Amer. Math. Soc. 149(2021), 199–207.CrossRefGoogle Scholar
Kallin, E., Fat polynomially convex sets . 1966 Function algebras (Proc. Internat. Sympos. on Function Algebras, Tulane Univ., 1965), pp. 149–152 Scott-Foresman, Chicago, III.Google Scholar
Lehto, O., On the first boundary value problem for functions harmonic in the unit circle. Ann. Acad. Sci. Fenn. Ser. A. I. 1955(1955), no. 210, 26 pp.Google Scholar
Noshiro, K., Cluster sets, Ergebnisse der Mathematik und ihrer Grenzgebiete. N. F., Heft, 28, Springer, Berlin, Göttingen, and Heidelberg, 1960.Google Scholar
Rudin, W.. Real and complex analysis. 3rd ed. McGraw-Hill, New York, 1987.Google Scholar
Wage, M. L., A generalization of Lusin's theorem. Proc. Amer. Math. Soc. 52(1975), 327–332.Google Scholar