Published online by Cambridge University Press: 10 December 2021
We define certain arithmetic derivatives on
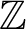 $\mathbb {Z}$
that respect the Leibniz rule, are additive for a chosen equation
$\mathbb {Z}$
that respect the Leibniz rule, are additive for a chosen equation
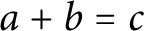 $a+b=c$
, and satisfy a suitable nondegeneracy condition. Using Geometry of Numbers, we unconditionally show their existence with controlled size. We prove that any power-saving improvement on our size bounds would give a version of the
$a+b=c$
, and satisfy a suitable nondegeneracy condition. Using Geometry of Numbers, we unconditionally show their existence with controlled size. We prove that any power-saving improvement on our size bounds would give a version of the
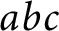 $abc$
Conjecture. In fact, we show that the existence of sufficiently small arithmetic derivatives in our sense is equivalent to the
$abc$
Conjecture. In fact, we show that the existence of sufficiently small arithmetic derivatives in our sense is equivalent to the
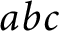 $abc$
Conjecture. Our results give an explicit manifestation of an analogy suggested by Vojta in the eighties, relating Geometry of Numbers in arithmetic to derivatives in function fields and Nevanlinna theory. In addition, our construction formalizes the widespread intuition that the
$abc$
Conjecture. Our results give an explicit manifestation of an analogy suggested by Vojta in the eighties, relating Geometry of Numbers in arithmetic to derivatives in function fields and Nevanlinna theory. In addition, our construction formalizes the widespread intuition that the
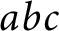 $abc$
Conjecture should be related to arithmetic derivatives of some sort.
$abc$
Conjecture should be related to arithmetic derivatives of some sort.
This research was supported by ANID (ex CONICYT) FONDECYT Regular grant 1190442 from Chile.