Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T06:44:53.995Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation and the Topology of Rationally Convex Sets

Published online by Cambridge University Press:  20 November 2018

E. S. Zeron
E. S. Zeron*
Affiliation:
Depto. Matemáticas, CIVESTAV, Apdo. Postal 14-740, México DF, 07000, México, and Centre de Recherches Mathématiques, Université de Montréal, Succ. Centre-ville, CP 6128, Montréal, H3C 3J7 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Considering a mapping 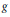$g$ holomorphic on a neighbourhood of a rationally convex set 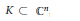$K\subset {{\mathbb{C}}^{n}}$, and range into the complex projective space 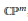$\mathbb{C}{{\mathbb{P}}^{m}}$, the main objective of this paper is to show that we can uniformly approximate 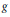$g$ on 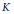$K$ by rational mappings defined from 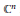${{\mathbb{C}}^{n}}$ into 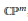$\mathbb{C}{{\mathbb{P}}^{m}}$. We only need to ask that the second Čech cohomology group 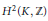${{\overset{\scriptscriptstyle\smile}{H}}^{2}}\left( K,\mathbb{Z} \right)$ vanishes.

Keywords

32E3032Q55Rationally convexcohomology and homotopy
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 4 , 01 December 2006 , pp. 628 - 636
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Aguilar, M. A., Gitler, S. and Prieto, C., Topología algebraica, un enfoque homotópico. McGraw-Hill, México, 1998.Google Scholar
[2] Alexander, H. and Wermer, J., Several Complex Variables and Banach Algebras. Third edition. Graduate Texts in Mathematics 35, Springer-Verlag, New York, 1998.Google Scholar
[3] Bredon, G. E.. Topology and Geometry. Graduate Texts in Mathematics 139, Springer-Verlag, New York, 1993.Google Scholar
[4] Dodson, C. T. J. and Parker, P. E., A User's Guide to Algebraic Topology. Mathematics and Its Applications 387, Kluwer, Dordrecht, 1997.Google Scholar
[5] Forstnerič, F., The Oka principle for sections of subelliptic submersions. Math. Z. 241(2002), no. 3, 527–551.Google Scholar
[6] Forstnerič, F. and Prezelj, J., Oka's principle for holomorphic submersions with sprays. Math. Ann. 322(2002), no. 4, 633–666.Google Scholar
[7] Gamelin, T. W., Uniform Algebras. Prentice-Hall, Englewood Cliffs, NJ, 1969.Google Scholar
[8] Gauthier, P. M. and Zeron, E. S., Approximation by rational mappings, via homotopy theory. Canad. Math. Bull. 49(2006), no. 2, 237–246.Google Scholar
[9] Grauert, H., Holomorphe Funktionen mit Werten in komplexen Lieschen Gruppen. Math. Ann. 133(1957), 450–472.Google Scholar
[10] Grauert, H. and Kerner, H., Approximation von holomorphen Schnittflächen in Faserbündeln mit homogener Faser. Arch. Math. 14(1963), 328–333.Google Scholar
[11] Gray, B., Homotopy Theory. An Introduction to Algebraic Topology. Pure and Applied Mathematics 64, Academic Press, New York, 1975.Google Scholar
[12] Hörmander, L. and Wermer, J., Uniform approximation on compact sets in ℂ n . Math. Scand. 23(1968), 5–21.Google Scholar
[13] Kuratowski, K., Topology. Vol. II. Academic Press, New York, 1968.Google Scholar
[14] Massey, W. S., Homology and Cohomology Theory. An Approach Based on Alexander-Spanier Cochains. Monographs and Textsbooks in Pure and Applied Mathematics 46, Marcel Dekker, New York, 1978.Google Scholar
[15] Milnor, J., Morse Theory. Annals of Mathematics Studies 51, Princeton University Press, Princeton NJ, 1963.Google Scholar
[16] Nirenberg, R. and Wells, R. O. Jr., Approximation theorems on differentiable submanifolds of a complex manifold. Trans. Amer.Math. Soc. 142(1969), 15–35.Google Scholar
[17] Oka, K.. Sur les fonctions des plusieurs variables. III: Deuxième problème de Cousin. J. Sc. Hiroshima Univ. 9(1939), 7–19.Google Scholar
[18] Sklyarenko, E. G., Homology and cohomology theories of general spaces. General topology, II, Encyclopaedia Math. Sci. 50, Springer, Berlin, 1996, pp. 119–256.Google Scholar
[19] Spanier, E. H., Algebraic Topology. McGraw-Hill, New York, 1966.Google Scholar