Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T01:46:58.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Application of Measure of Noncompactness to Infinite Systems of Differential Equations

Published online by Cambridge University Press:  20 November 2018

M. Mursaleen
M. Mursaleen*
Affiliation:
Department of Mathematics, Aligarh Muslim University, Aligarh-202002, India e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

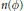In this paper we determine theHausdorff measure of noncompactness on the sequence space $n\left( \phi \right)$ of 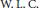$\text{W}\text{.}\,\text{L}\text{.}\,\text{C}.$ Sargent. Further we apply the technique of measures of noncompactness to the theory of infinite systems of differential equations in the Banach sequence spaces 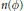$n\left( \phi \right)$ and 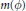$m\left( \phi \right)$. Our aim is to present some existence results for infinite systems of differential equations formulated with the help of measures of noncompactness.

Keywords

46B1546B4546B5034A3434G20sequence spacesBK spacesmeasure of noncompactnessinfinite system of differential equations
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 388 - 394
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Banaś, J. and Goebel, K., Measures of noncompactness in Banach spaces. Lecture Notes in Pure and Applied Mathematics 60, Marcel Dekker, New York and Basel, 1980.Google Scholar
[2] Banaś, J. and Lecko, M., Solvability of infinite systems of differential equations in Banach sequence spaces. J. Comput. Appl. Math. 137(2001), 363–375. http://dx.doi.org/10.1016/S0377-0427(00)00708-1 Google Scholar
[3] Bellman, R., Methods of Nonlinear Analysis II. Academic Press, New York, 1973.Google Scholar
[4] Deimling, K., Ordinary differential equations in Banach spaces. Lecture Notes in Mathematics 596, Springer, Berlin, 1977.Google Scholar
[5] Gohberg, I. T., Goldenštein, L. S. and Markus, A. S., Investigations of some properties of bounded linear operators with their q-norms. (Russian) UČen. Zap. Kishinev. Univ. 29(1957), 29–36. Google Scholar
[6] Hille, E., Pathology of infinite systems of linear first order differential equations with constant coefficient. Ann. Mat. Pure Appl. 55(1961), 135–144. http://dx.doi.org/10.1007/BF02412080 Google Scholar
[7] de Malafosse, B. and V. RakoČević, Application of measure of noncompactness in operators on the spaces s0αs(c) α s(c) p. J. Math. Anal. Appl. 323(2006), 131–145. http://dx.doi.org/10.1016/j.jmaa.2005.10.024 Google Scholar
[8] Malkowsky, E. and Mursaleen, M., Matrix transformations between FK-spaces and the sequence spaces mϕ and nϕ. J. Math. Anal. Appl. 196(1995), 659–665. http://dx.doi.org/10.1006/jmaa.1995.1432 Google Scholar
[9] Mursaleen, M., On some geometric properties of a sequence space related to lp. Bull. Austral. Math. Soc. 67(2003), 343–347. http://dx.doi.org/10.1017/S0004972700033803 Google Scholar
[10] Mursaleen, M. and Noman, A. K., Compactness by the Hausdorff measure of noncompactness. Nonlinear Anal. 73(2010), 2541–2557. http://dx.doi.org/10.1016/j.na.2010.06.030 Google Scholar
[11] Mursaleen, M. and Noman, A. K., Applications of the Hausdorff measure of noncompactness in some sequence spaces of weighted means. Comput. Math. Appl. 60(2010), 1245–1258. http://dx.doi.org/10.1016/j.camwa.2010.06.005 Google Scholar
[12] Persidskii, K. P., Countable system of differential equations and stability of their solutions. Izv. Akad. Nauk Kazach. SSR 7(1959), 52–71. Google Scholar
[13] Persidski, K. P., Countable systems of differential equations and stability of their solutions III: Fundamental theorems on stability of solutions of countable many differential equations. Izv. Akad. Nauk. Kazach. SSR 9(1961), 11–34. Google Scholar
[14] Sargent, W. L. C., Some sequence spaces related to the lp spaces. J. London Math. Soc. 35(1960), 161–171. http://dx.doi.org/10.1112/jlms/s1-35.2.161 Google Scholar
[15] Szufla, S., On the existence of solutions of differential equations in Banach spaces. Bull. Acad. Polon. Sci. Sér. Sci. Math. 30(1982), 507–515. Google Scholar
[16] Voigt, A., Line method approximations to the Cauchy problem for nonlinear parabolic differential equations. Numer. Math. 23(1974), 23–36. http://dx.doi.org/10.1007/BF01409988 Google Scholar
[17] Walter, W., Differential and Integral Inequalities. Springer, Berlin, 1970.Google Scholar
[18] Zautykov, O. A., Denumerable systems of differential equations and their applications. (Russian) Differencial’nye Uravnenija 1(1965), 162–170. Google Scholar
[19] Zautykov, O. A. and Valeev, K. G., Infinite systems of differential equations. Izdat. Nauka Kazah. SSR, Alma-Ata, 1974.Google Scholar