Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
De Filippis, Vincenzo
and
Wei, Feng
2018.
b-Generalized Skew Derivations on Lie Ideals.
Mediterranean Journal of Mathematics,
Vol. 15,
Issue. 2,
Ali, Shakir
Dhara, Basudeb
Fahid, Brahim
and
Raza, Mohd Arif
2019.
On Semi(prime) Rings and Algebras with Automorphisms and Generalized Derivations.
Bulletin of the Iranian Mathematical Society,
Vol. 45,
Issue. 6,
p.
1805.
Raza, Mohd Arif
Ali, Shakir
and
Alhazmi, Husain
2021.
m-potent commutators of skew derivations on Lie ideals.
Georgian Mathematical Journal,
Vol. 28,
Issue. 6,
p.
937.
Carini, Luisa
and
De Filippis, Vincenzo
2022.
Algebra and Related Topics with Applications.
Vol. 392,
Issue. ,
p.
59.
Liu, Cheng-Kai
and
Tsai, Yuan-Tsung
2022.
Annihilators of power values of derivations on Lie ideals of prime rings.
Journal of Algebra and Its Applications,
Vol. 21,
Issue. 10,
Raza, Mohd Arif
Khan, Abdul Nadim
and
Alhazmi, Husain
2022.
A characterization of $ b- $generalized derivations on prime rings with involution.
AIMS Mathematics,
Vol. 7,
Issue. 2,
p.
2413.
Dhara, B.
Kar, S.
and
Bera, M.
2022.
X-generalized skew derivations with annihilating and centralizing conditions in prime rings.
ANNALI DELL'UNIVERSITA' DI FERRARA,
Vol. 68,
Issue. 1,
p.
147.
Liu, Cheng-Kai
and
Tsai, Yuan-Tsung
2022.
Derivations with annihilator conditions on multilinear polynomials.
Linear and Multilinear Algebra,
Vol. 70,
Issue. 12,
p.
2397.
Bera, Nripendu
Dhara, Basudeb
and
Kar, Sukhendu
2023.
A result concerning b-generalized skew derivations on multilinear polynomials in prime rings.
Communications in Algebra,
Vol. 51,
Issue. 3,
p.
887.
Carini, Luisa
and
Scudo, Giovanni
2023.
On Posner’s theorem with b-generalized skew derivations on Lie ideals.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 03,
Abdullah, Ali Ahmed
and
Khan, Nazim
2024.
X
-generalized skew derivations behaving as weak Jordan right
η
-centralizers in prime rings
.
Communications in Algebra,
Vol. 52,
Issue. 2,
p.
817.
Dhara, Basudeb
Tiwari, Shailesh Kumar
Gupta, Pallavee
and
Bera, Manami
2025.
Annihilating co-commutators of
b
-generalized skew derivations in prime rings
.
Communications in Algebra,
p.
1.
Bera, Nripendu
Dhara, Basudeb
and
Kar, Sukhendu
2025.
Study of commutator involving X-generalized skew derivations and annihilators in prime rings.
Asian-European Journal of Mathematics,
Vol. 18,
Issue. 01,
Dhara, Basudeb
Kar, Sukhendu
and
Ghosh, Sourav
2025.
Product of commutators with b-generalized skew derivations on Lie ideals.
Communications in Algebra,
p.
1.
Bera, Nripendu
and
Dhara, Basudeb
2025.
b
-generalized skew derivations acting on multilinear polynomials in prime rings
.
Communications in Algebra,
Vol. 53,
Issue. 2,
p.
761.
 $R$ be a prime ring of characteristic diòerent from
$R$ be a prime ring of characteristic diòerent from  $2$, let
$2$, let 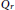 ${{Q}_{r}}$ be its right Martindale quotient ring, and let
${{Q}_{r}}$ be its right Martindale quotient ring, and let  $C$ be its extended centroid. Suppose that
$C$ be its extended centroid. Suppose that  $F$ is a generalized skew derivation of
$F$ is a generalized skew derivation of 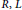 $R,\,L$ a non-central Lie ideal of
$R,\,L$ a non-central Lie ideal of 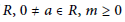 $R,\,0\,\ne \,a\,\in \,R,\,m\,\ge \,0$ and
$R,\,0\,\ne \,a\,\in \,R,\,m\,\ge \,0$ and 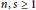 $n,\,s\,\ge \,1$ fixed integers. If
$n,\,s\,\ge \,1$ fixed integers. If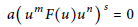 $$a{{\left( {{u}^{m}}F\left( u \right){{u}^{n}} \right)}^{s}}\,=\,0$$
$$a{{\left( {{u}^{m}}F\left( u \right){{u}^{n}} \right)}^{s}}\,=\,0$$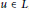 $u\,\in \,L$, then either
$u\,\in \,L$, then either 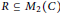 $R\,\subseteq \,{{M}_{2}}\left( C \right)$, the ring of
$R\,\subseteq \,{{M}_{2}}\left( C \right)$, the ring of 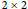 $2\,\times \,2$ matrices over
$2\,\times \,2$ matrices over  $C$, or
$C$, or 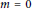 $m\,=\,0$ and there exists
$m\,=\,0$ and there exists 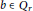 $b\,\in \,{{Q}_{r}}$ such that
$b\,\in \,{{Q}_{r}}$ such that 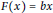 $F\left( x \right)\,=\,bx$, for any
$F\left( x \right)\,=\,bx$, for any 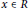 $x\,\in \,R$, with
$x\,\in \,R$, with 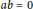 $ab\,=\,0$.
$ab\,=\,0$.