Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-22T21:16:28.787Z Has data issue: false hasContentIssue false
  • English
  • Français

An N-Parameter Chebyshev Set which is not a Sun

Published online by Cambridge University Press:  20 November 2018

Dietrich Braess
Dietrich Braess*
Affiliation:
Institut Für Mathematik Ruhr-Universitât Bochum463 Bochum, F. R., Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently, Dunham has given examples for 1-parameter and 2-parameter Chebyshev sets which are not suns. In this note 2-parameter sets with these properties are described.

When studying the old problem whether Chebyshev sets are always convex, Klee [10] introduced certain sets which were called suns by Efimov and Stechkin [7]. Recently, in two shorts notes Dunham [4, 5] has given examples of 1-parameter- and 2-parameter-sets which are Chebyshev sets but not suns (cf. also [3]). The examples refer to Chebyshev sets in 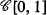containing an isolated point.

Keywords

Convexity of Chebyshev sets41 A 6541 A 50
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 4 , October 1975 , pp. 489 - 492
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Braess, D., Kritische Punkte bei der nichtlinearen Tschebyscheff-Approximation. Math. Z. 132(1973), 327–341.Google Scholar
2. Braess, D., On varisolvency and alternation, J. Approximation Theory 12 (1974), 230–233.Google Scholar
3. Brosowski, B., Deutsch, F., Lambert, J. and Morris, P. D., Chebyshev sets which are not suns, Math. Annalen 212 (1974), 89–101.Google Scholar
4. Dunham, C. B., Chebyshev sets in which are not suns, Canad. Math. Bull. (1) 18 (1975), 35–38.Google Scholar
5. Dunham, C. B., A 2-parameter Chebyshev set in which is not a sun, Proc. Amer. Math. Soc. (to appear).Google Scholar
6. Dunham, C. B., Necessity of alternation, Canad. Math. Bull. 11 (1968), 743–744.Google Scholar
7. Efimov, N. V. and Stechkin, S. B., Some properties of Chebyshev sets (Russian) Dokl. Akad. Nauk SSSR 118 (1958), 17–19.Google Scholar
8. Hurewicz, W. and Wallmann, H., Dimension Theory, Princeton University Press, Princeton 1948.Google Scholar
9. Karlin, S., Total Positivity I, Stanford University Press, Stanford 1968.Google Scholar
10. Klee, V., A characterization of convex sets, Amer. Math Monthly 56 (1949), 247–249.Google Scholar
11. Meinardus, G., Approximation of Functions: Theory and Numerical Methods, Springer, Berlin-Heidelberg-New York 1967.Google Scholar
12. Rice, J. R., The Approximation of Functions 2, Nonlinear and Multivariate Theory, Addison-Wesley, Reading 1969.Google Scholar
13. Wulbert, D., Uniqueness and differential characterization of approximations from manifolds of functions, Amer. J. Math. 93 (1971), 350–366.Google Scholar