Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T16:36:51.053Z Has data issue: false hasContentIssue false
  • English
  • Français

An Integral Representation for the Generalized Binomial Function

Published online by Cambridge University Press:  20 November 2018

M. Heggie  and
G. R. Nicklason
M. Heggie
Affiliation:
Sydney, Nova Scotia, B1P 6L2 e-mail:[email protected]
G. R. Nicklason
Affiliation:
Sydney, Nova Scotia, B1P 6L2 e-mail:[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The generalized binomial function 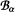can be obtained as the solution of the equation y = 1 +zyα which satisfies y(0) = 1 where α ≠ 1 is assumed to be real and positive. The technique of Lagrange inversion can be used to express 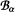as a series which converges for |z| < α-α|a — l|α-1. We obtain a representation of the function as a contour integral and show that if α > 1 it is an analytic function in the complex z plane cut along the nonnegative real axis. For 0 < α < 1 the region of analyticity is the sector |arg(—z)| < απ. In either case 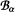defined by the series can be continued beyond the circle of convergenece of the series through a functional equation which can be derived from the integral representation.

Keywords

30E2033C20contour integral representationanalytic continuationgeneralized hypergeometric functionMellin-Barnes integral
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 39 , Issue 1 , 01 March 1996 , pp. 59 - 67
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Graham, R. L., Knuth, D. E. and Patashnik, O., Concrete mathematics, Addison-Wesley, New York (1989), 200.Google Scholar
2. Heggie, M. and Nicklason, G. R., Quadrature of an exact shock solution and the generalized binomial function; preprint.Google Scholar
3. Heggie, M. and Nicklason, G. R., The generalized binomial function and “singular hyperelliptic “ integrals; preprint.Google Scholar
4. Loiseau, J. F., Codaccioni, J. P. and R. Caboz, Incomplete hyperelliptic integrals and hypergeometric series, Math, of Comp. 53(1989), 335–342.Google Scholar
5. Nicklason, G. R. and Heggie, M., An exact shock solution, Can. Appl. Math. Quart. 1(1993), 221–254.Google Scholar
6. Nicklason, G. R. and Heggie, M., Application of the generalized binomial function to one-dimensional shock problems; preprint.Google Scholar
7. Rainville, E. D., Special functions, Chelsea, New York, 1971.Google Scholar
8. Whittaker, E. T. and Watson, G. N., A course in modern analysis, 4th éd., Cambridge Univ. Press, New York, 1927.Google Scholar