Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-14T12:30:36.964Z Has data issue: false hasContentIssue false
  • English
  • Français

An Integral for Cesàro Summable Series

Published online by Cambridge University Press:  20 November 2018

George Cross
George Cross*
Affiliation:
University of Waterloo
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The pk+2 - integral of James [2] is strong enough to integrate a trigonometric series of the form

1.1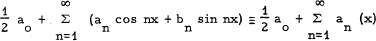

which is summable (C, k) in [0,2π], provided an extra condition holds involving the conjugate series

1.2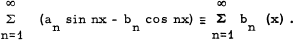

Considering series with coefficients o(n), Taylor [5] constructed an integral (the AP-integral) which successfully integrates series of the form (1. 1) which are Abel summable provided an extra condition holds involving the Abel means of the conjugate series (1.2).

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 10 , Issue 1 , April 1967 , pp. 85 - 97
Copyright
Copyright © Canadian Mathematical Society 1967

Footnotes

1

The results in this paper were obtained while the author was a fellow of the Summer Research Institute (Kingston) of the Canadian Mathematical Congress, 1965.

References

1. Hardy, G. H., Divergent Series. Oxford (1944).Google Scholar
2. James, R. D., Generalized nth Primitives. Trans. Amer. Math. Soc. vol. 76 (1955), pages 149-176.Google Scholar
3. James, R. D., Summable Trigonometric Series. Pacific J. Math. 6 (1955), pages 99-110.Google Scholar
4. Jeffery, R. L., Trigonometric Series. Toronto (1955).Google Scholar
5. Taylor, S. J., An Integral of Perron ‘ s Type. Quart. J.Math. Oxford (2). vol. 6 (1955), pages 255-274.Google Scholar
6. Verblunsky, S., On the Theory of Trigonometric Series II. Proc. London Math. Soc. 34(1933), pages 457-491.Google Scholar
7. Verblunsky, S., On the Theory of Trigonometric Series VI. Proc. London Math. Soc. 38 (1933), pages 284-326.Google Scholar
8. Zygmund, A., Trigonometric Series. (2nd è d., Cambridge, 1958) I.Google Scholar
9. Zygmund, A., Trigonometric Series. (2nd èd., Cambridge, 1958) II.Google Scholar