Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T17:03:16.393Z Has data issue: false hasContentIssue false
  • English
  • Français

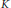An Inductive Limit Model for the $K$-Theory of the Generator-Interchanging Antiautomorphism of an Irrational Rotation Algebra

Published online by Cambridge University Press:  20 November 2018

P. J. Stacey
P. J. Stacey*
Affiliation:
Department of Mathematics La Trobe University Victoria 3086 Australia, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 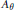${{A}_{\theta }}$ be the universal 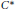${{C}^{*}}$-algebra generated by two unitaries 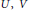$U,\,V$ satisfying $VU\,=\,{{e}^{2\pi i\theta }}UV$ and let 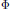$\Phi $ be the antiautomorphism of 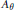${{A}_{\theta }}$ interchanging 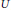$U$ and 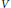$V$. The 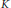$K$-theory of 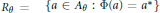${{R}_{\theta }}\,=\,\{a\,\in \,{{A}_{\theta }}\,:\,\Phi (a)\,=\,{{a}^{*}}\}$ is computed. When 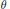$\theta $ is irrational, an inductive limit of algebras of the form 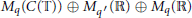${{M}_{q}}(C(\mathbb{T}))\,\oplus \,{{M}_{{{q}'}}}(\mathbb{R})\,\oplus \,{{M}_{q}}(\mathbb{R})$ is constructed which has complexification 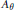${{A}_{\theta }}$ and the same 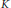$K$-theory as 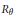${{R}_{\theta }}$.

Keywords

46L3546L80
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 3 , 01 September 2003 , pp. 441 - 456
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Blackadar, B., K-theory for operator algebras. Springer-Verlag, New York, 1986.Google Scholar
[2] Boca, F. P., On the flip fixed point algebra in certain noncommutative tori. Indiana Univ. Math. J. 45 (1996), 253–273.Google Scholar
[3] Boca, F. P., Projections in rotation algebras and theta functions. Comm. Math. Phys. 202 (1999), 325–357.Google Scholar
[4] Bratteli, O., Elliott, G. A., Evans, D. E. and Kishimoto, A., Non-commutative spheres II: rational rotations. J. Operator Theory 27 (1992), 53–85.Google Scholar
[5] Cuntz, J., K-theory and C*-algebras. In: Springer Lecture Notes in Math. 1046, 55–79, Springer-Verlag, Berlin, 1984.Google Scholar
[6] Elliott, G. A. and Evans, D., The structure of the irrational rotation C*-algebra. Ann. of Math. 138 (1993), 477–501.Google Scholar
[7] Eliott, G. A. and Lin, Q., Cut-down method in the inductive limit decomposition of non-commutative tori. J. LondonMath. Soc. (2) 54 (1996), 121–134.Google Scholar
[8] Karoubi, M., K-theory: an introduction. Springer-Verlag, New York, Berlin, Heidelberg, 1978.Google Scholar
[9] Rieffel, M. A., Projective modules over higher-dimensional non-commutative tori. Canad. J. Math. XL(1988), 257–338.Google Scholar
[10] Schröder, H., K-theory for real C*-algebras and applications. Longman, Harlow, 1993.Google Scholar
[11] Stacey, P. J., Stability of involutory *-antiautomorphisms in UHF-algebras. J. Operator Theory 24 (1990), 57–74.Google Scholar
[12] Stacey, P. J., Inductive limit toral automorphisms of irrational rotation algebras. Canad. Math. Bull. 44 (2001), 335–336.Google Scholar
[13] Stacey, P. J., Inductive limit decompositions of real structures in irrational rotation algebras. Indiana Univ. Math. J. 51 (2002), 1511–1540.Google Scholar
[14] Walters, S., Inductive limit automorphisms of the irrational rotation algebra. Comm. Math. Phys. 171 (1995), 365–381.Google Scholar
[15] Walters, S., K-theory of non-commutative spheres arising from the Fourier automorphism. Canad. J. Math. (3) 53 (2001), 631–672.Google Scholar
[16] Walters, S., On the inductive limit structure of order four automorphisms of the irrational rotation algebra. Internat. J. Math., to appear.Google Scholar
[17] Yin, H.-S., A simple proof of the classification of rational rotation C*-algebras. Proc. Amer.Math. Soc. 98 (1986), 469–470.Google Scholar