No CrossRef data available.
Article contents
An Improved Wintner Oscillation Criterion for Second Order Linear Differential Equations
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
An iterative technique is used to establish an oscillation theorem for the equation x″+ a(t)x=0 which relaxes the condition that a(t) satisfy
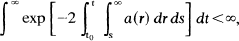
without the restriction that
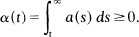
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1984
References
1.
Hartman, P., On Nonoscillatory Differential Equations of Second Order, Amer. J. Math., Vol. 74 (1952), pp. 389-400.Google Scholar
3.
Kamenev, I. V., Criteria for a Second Order Linear Equation to be Oscillatory, Related to the Existence of a Principal Solution, Differentsial'nye Uravneniya, Vol. 9, No 2 (1973), pp. 370-373.Google Scholar
4.
Leighton, W. and Morse, M., Singular Quadratic Functionals, Trans. Am. Math. Soc, Vol. 40 (1936), pp. 252-286.Google Scholar
5.
Wintner, A., On the Non-existence of Conjugate Points, Am. J. Math Vol. 73 (1951), pp. 368-380.
Google Scholar


