Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2025-01-03T18:14:57.571Z Has data issue: false hasContentIssue false
  • English
  • Français

An Extrapolation Theorem for Contractions with Fixed Points

Published online by Cambridge University Press:  20 November 2018

Ryotaro Sato
Ryotaro Sato*
Affiliation:
Department of Mathematics, Okayama University Okayama, 700, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [9] de la Torre proved that if 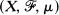is a finite measure space and T is a linear operator on a real 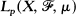for some fixed p, 1 < p < ∞ , such that ||T||P ≤ 1 and simultaneously ||T||∞ ≤ l, and also such that there exists 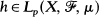with Th = h and h≠0 a.e., then the dominated ergodic theorem holds for T, i.e. for every 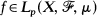we have

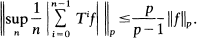
de la Torre proved his result, by showing that the operator S, defined by Sf = (sgn h) - T(f • sgn h) for is positive, and by applying Akcoglu's theorem [1] to S.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 24 , Issue 2 , 01 June 1981 , pp. 199 - 203
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Akcoglu, M. A.: A pointwise ergodic theorem in Lp-spaces, Canad. J. Math.. 27 (1975), 1075-1082.Google Scholar
2. Akcoglu, M. A. and Brunei, A.: Contractions on L1-spaces, Trans. Amer. Math. Soc.. 155 (1971), 315-325.Google Scholar
3. Akcoglu, M. A. and Chacon, R. V.: A convexity theorem for positive operators, Z. Wahrscheinlichkeitstheorie und Verw. Gebiete. 3 (1965), 328-332.Google Scholar
4. Chacon, R. V. and Krengel, U.: Linear modulus of a linear operator, Proc. Amer. Math. Soc.. 15 (1964), 553-559.Google Scholar
5. Dunford, N. and Schwartz, J. T.: Convergence almost everywhere of operator averages, J. Rational Mech. Anal.. 5 (1956), 129-178.Google Scholar
6. Dunford, N. and Schwartz, J. T.: Linear operators. Part I: General theory, New York, 1958.Google Scholar
7. Foguel, S. R.: The ergodic theory of Markov processes, New York, 1969.Google Scholar
8. Garsia, A. M. Topics in almost everywhere convergence, Chicago, 1970.Google Scholar
9. de la Torre, A. A dominated ergodic theorem for contractions with fixed points, Canad. Math. Bull.. 20 (1977), 89-91.Google Scholar