Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Coulhon, Thierry
and
Saloff-Coste, Laurent
1991.
Semi-groupes d'opérateurs et espaces fonctionnels sur les groupes de Lie.
Journal of Approximation Theory,
Vol. 65,
Issue. 2,
p.
176.
Coulhon, Thierry
1992.
In�galit�s de Gagliardo-Nirenberg pour les semi-groupes d'op�rateurs et applications.
Potential Analysis,
Vol. 1,
Issue. 4,
p.
343.
Gressman, Philip T.
2007.
Sharp Lp–Lq estimates for generalized k-plane transforms.
Advances in Mathematics,
Vol. 214,
Issue. 1,
p.
344.
Kumar, Ashisha
and
Ray, Swagato K.
2010.
Mixed norm estimate for Radon transform on weighted L p spaces.
Proceedings - Mathematical Sciences,
Vol. 120,
Issue. 4,
p.
441.
Kumar, Ashisha
and
Ray, Swagato K.
2012.
Weighted estimates for the k-plane transform of radial functions on euclidean spaces.
Israel Journal of Mathematics,
Vol. 188,
Issue. 1,
p.
25.
Rubin, B.
2019.
Norm estimates for k-plane transforms and geometric inequalities.
Advances in Mathematics,
Vol. 349,
Issue. ,
p.
29.


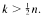 Specifically let
Specifically let