The main result of this paper is a theorem about three conies in the complex or the real complexified projective plane. Is this theorem new? We have never seen it anywhere before. But since the golden age of projective geometry so much has been published about conies that it is unlikely that no one noticed this result. On the other hand, why does it not appear in the literature? Anyway, it seems interesting to "repeat" this property, because several theorems in connection with straight lines and (or) conies in projective, affine or euclidean planes are in fact special cases of this theorem. We give a few classical examples: the theorems of Pappus-Pascal, Desargues, Pascal (or its converse), the Brocard points, the point of Miquel. Finally, we have never seen in the literature a proof of these theorems using the same short method 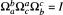see the proof of the main theorem).