Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T00:30:15.895Z Has data issue: false hasContentIssue false
  • English
  • Français

An Asymptotic Formula for Reciprocals of Logarithms of Certain Multiplicative Functions

Published online by Cambridge University Press:  20 November 2018

Jean-Marie de Koninck  and
Aleksandar Ivić
Jean-Marie de Koninck
Affiliation:
Départment de Mathématiques, Université Laval, Québec, P.Q. Canada, G IK 7P4
Aleksandar Ivić
Affiliation:
Rudarsko-Geološki Fakultet, Djušina 7, 11000 Beograd, Yugoslavia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Sums of the form 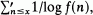where f(n) is a multiplicative arithmetical function and 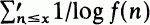denotes summation over those values of n for which f(n)>0 and f(n) ≠1, were studied by De Koninck [2], De Koninck and Galambos [3], Brinitzer [1] and Ivič [5]. The aim of this note is to give an asymptotic formula for 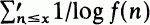a certain class of multiplicative, positive, primeindependent functions (an arithmetical function is prime-independent if f(pv) = g(v) for all primes p and v = 1, 2, …). This class of functions includes, among others, the functions a(n) and τ(e)(n), which represent the number of nonisomorphic abelian groups of order n and the number of exponential divisors of n respectively, and none of the estimates of the above-mentioned papers may be applied to this class of functions. We prove the following.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 21 , Issue 4 , 01 December 1978 , pp. 409 - 413
Copyright
Copyright © Canadian Mathematical Society 1978

References

1. Brinitzer, E., Eine asymptotische Formel für Summen über die reziproken Werte additiver Funktionen, Acta Arith. XXXII, 1977, pp. 387-391.Google Scholar
2. De Koninck, J.-M., On a class of arithmetical functions, Duke Math. Journal, 39, 1972, pp. 807-818.Google Scholar
3. De Koninck, J.-M. and Galambos, J., Sums of reciprocals of additive functions, Acta Arith. XXV, 1974, pp. 159-164.Google Scholar
4. Herstein, I. N., Topics in Algebra, Blaisdell, Waltham, Mass.-Toronto-London, 1964.Google Scholar
5. Ivic, A., The distribution of values of some multiplicative functions, Publications de l'institut Math. (Belgrade), 22 (36), 1977, pp. 87-94.Google Scholar
6. Knopfmacher, J., Abstract Analytic Number Theory, North-Holland/American Elsevier, Amsterdam-Oxford, 1975.Google Scholar
7. Selberg, A., Note on a paper by L. G. Sathe, J. Indian Math. Soc, 18, 1954, pp. 83-87.Google Scholar
8. Subbarao, M. V., On some arithmetic convolutions in the theory of arithmetic functions, Lecture Notes in Math. 251, Springer-Verlag, Berlin-Heidelberg-New York, 1972, pp. 247-271.Google Scholar
9. Walfisz, A., Weylsche Exponentialsummen in der neueren Zahlentheorie, VEB Verlag, Berlin, 1963, pp. 192-198.Google Scholar