Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T20:19:09.144Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost Sure Global Well-posedness for the Fractional Cubic Schrödinger Equation on the Torus

Published online by Cambridge University Press:  20 November 2018

Seckin Demirbas
Seckin Demirbas*
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61801, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a previous paper, we proved that the 1-d periodic fractional Schrödinger equation with cubic nonlinearity is locally well-posed in 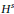${{H}^{s}}$ for 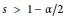$s>1-\alpha /2$ and globally well-posed for 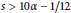$s>10\alpha -1/12$. In this paper we define an invariant probability measure $\mu$ on 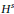${{H}^{s}}$ for 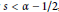$s<\alpha -1/2$, so that for any 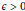$\text{ }\!\!\varepsilon\!\!\text{ }>0$ there is a set 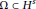$\Omega \subset {{H}^{s}}$ such that 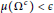$\mu \left( {{\Omega }^{c}} \right)<\text{ }\!\!\varepsilon\!\!\text{ }$ and the equation is globally well-posed for initial data in 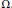$\Omega$. We see that this fills the gap between the local well-posedness and the global well-posedness range in an almost sure sense for 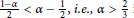$\frac{1-\alpha }{2}<\alpha -\frac{1}{2},i.e.,\alpha >\frac{2}{3}$ in an almost sure sense.

Keywords

35Q55NLSfractional Schrodinger equationalmost sure global wellposedness
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 3 , 01 September 2015 , pp. 471 - 485
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Bourgain, J., Fourier transform restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations. I. Schrôdingerequations. Geom. Funct. Anal. 3(1993), no. 2, 107–156. http://dx.doi.org/10.1007/BF01896020 Google Scholar
[2] Bourgain, J., Refinements of Strichartz’ inequality and applications to 2-D-NLS with critical nonlinearity. Internat. Math. Res. Notices. 5(1998), no. 5, 253–283.Google Scholar
[3] Bourgain, J., Periodic nonlinear Schrb'dinger equation and invariant measures. Comm. Math. Phys. 166(1994), no. 1, 1–26. http://dx.doi.org/10.1007/BF02099299 Google Scholar
[4] Bourgain, J. and Bulut, A., Gibbs measure evolution in radial nonlinear wave and Schrôdinger equations on the ball. C. R. Math. Acad. Sci. Paris. 350(2012), no. 11-12, 571–575. http://dx.doi.Org/10.101 6/j.crma.2O1 2.05.006 Google Scholar
[5] Bourgain, J. and Bulut, A., Invariant Gibbs measure evolution for the radial nonlinear wave equation on the 3d ball. J. Funct. Anal.266(2014), no. 4, 2319–2340. http://dx.doi.Org/10.1016/j.jfa.2013.06.002 Google Scholar
[6] Burq, N., Gerard, P., and Tzvetkov, N., An instability property of the nonlinear Schrôdingerequation on Sd. Math. Res. Lett. 9(2002), no. 2-3, 323–335. http://dx.doi.org/10.4310/MRL.2002.v9.n3.a8 Google Scholar
[7] Burq, N. and Tzvetkov, N., Invariant measure for a three dimensional nonlinear wave equation.Int. Math. Res. Not. IMRN 2007, no. 22, Art.ID rnmlO8.Google Scholar
[8] Catoire, F. and Wang, W-M., Bounds on Sobolev norms for the nonlinear Schrôdingerequation on general tori. Commun.Pure Appl. Anal. 9(2010), no. 2, 483–491. http://dx.doi.Org/10.3934/cpaa.2010.9.483 Google Scholar
[9] Cho, Y., Hwang, G., Kwon, S., and Lee, S., Well-posedness and ill-posedness for the cubic fractional Schrôdingerequations. arxiv:1311.0082Google Scholar
[10] Colliander, J. and Oh, T., Almost sure well-posedness of the cubic nonlinear Schrôdingerequation below L2(T). Duke Math. J. 161(2012), no. 3, 367–414. http://dx.doi.Org/10.1215/00127094-1507400 Google Scholar
[11] Demirbas, S., Local well-posedness for 2-D Schrôdingerequation on irrational tori and bounds on Sobolev norms. arxiv:1307.0051Google Scholar
[12] Demirbas, S., Erdogan, M. B., and Tzirakis, N., Existence and Uniqueness theory for the fractional Schrôdingerequation on the torus. arxiv:1312.5249Google Scholar
[13] Erdogan, M. B. and Tzirakis, N., Talbot effect for the cubic nonlinear Schrôdingerequation on the torus. Math. Res. Lett. 20(2013), 1081–1090. http://dx.doi.org/10.4310/MRL.2013.v20.n6.a7 Google Scholar
[14] Kirkpatrick, K., Lenzmann, E., and Staffilani, G., On the continuum limit for discrete NLS with long-range lattice interactions. Comm. Math. Phys. 317(2013), no. 3, 563–591. http://dx.doi.org/10.1007/s00220-012-1621-x Google Scholar
[15] Laskin, N., Fractional quantum mechanics and Levy path integrals. Phys. Lett. 268(2000), no. 4-6, 298–305. http://dx.doi.Org/10.101 6/S0375-9601 (00)00201 -2 Google Scholar
[16] Lebowitz, J. L., Rose, H. A., and Speer, E. R., Statistical mechanics of the nonlinear Schrôdinger equation. J. Statist. Phys. 50(1988), no. 3-4, 657–687. http://dx.doi.Org/10.1007/BF01026495 Google Scholar
[17] Nahmod, A. R., Oh, T., and Staffilani, G., Invariant weighted Wiener measures and almost sure global well-posedness for the periodic derivative NLS. J. Eur. Math. Soc. (JEMS). 14(2012), no. 4, 1275–1330. http://dx.doi.org/10.4171/JEMS/333 Google Scholar
[18] Nahmod, A. R., Pavlovic, N., and Staffilani, G., Almost sure existence of global weak solutions for supercriticalNavier-Stokes equations. SIAM J. Math.Anal.45(2013), no. 6, 3431–3452. http://dx.doi.Org/10.1137/120882184 Google Scholar
[19] Oh, T., Lecture notes. http://www.maths.ed.ac.uk/∼toh/Files/2008_11_27_Hiro_Oh_Gibbs_Measure_Lectures.pdf Google Scholar
[20] Oh, T., Invariant Gibbs measures and a.s. global well posedness for coupled KdV systems. Differential Integral Equations. 22(2009), no. 7-8, 637–668.Google Scholar
[21] Oh, T., Invariance of the Gibbs measure for the Schrodinger-Benjamin-Ono system. SIAM J. Math.Anal.41(2009/10), no. 6, 2207–2225.Google Scholar
[22] Richards, G., Invariance of the Gibbs measure for the periodic quartic gKdV. arxiv:12 09.4337Google Scholar
[23] Zhidkov, P., Korteweg-de Vries and nonlinear Schrodinger equations: qualitative theory. Lecture Notes in Mathematics, 1756, Springer-Verlag, Berlin, 2001.Google Scholar