Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T13:40:56.093Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost Everywhere Convergence of Convolution Measures

Published online by Cambridge University Press:  20 November 2018

Karin Reinhold ,
Anna K. Savvopoulou  and
Christopher M. Wedrychowicz
Karin Reinhold
Affiliation:
Department of Mathematics, University at Albany, SUNY, Albany, NY 12222 USAe-mail: [email protected]
Anna K. Savvopoulou
Affiliation:
Department of Mathematical Sciences, Indiana University in South Bend, South Bend, IN, 46545 USAe-mail: [email protected]: [email protected]
Christopher M. Wedrychowicz
Affiliation:
Department of Mathematical Sciences, Indiana University in South Bend, South Bend, IN, 46545 USAe-mail: [email protected]: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 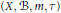$\left( X,\,\mathcal{B},\,m,\,\tau \right)$ be a dynamical system with 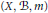$\left( X,\mathcal{B},m \right)$ a probability space and $\tau $ an invertible, measure preserving transformation. This paper deals with the almost everywhere convergence in 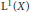${{\text{L}}^{1}}\left( X \right)$ of a sequence of operators of weighted averages. Almost everywhere convergence follows once we obtain an appropriate maximal estimate and once we provide a dense class where convergence holds almost everywhere. The weights are given by convolution products of members of a sequence of probability measures 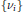$\left\{ {{v}_{i}} \right\}$ defined on $\mathbb{Z}$. We then exhibit cases of such averages where convergence fails.

Keywords

28D
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 4 , 01 December 2012 , pp. 830 - 841
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Akcoglu, M. A., Alternating sequences with nonpositive operators. Proc. Amer. Math. Soc. 104(1988), no. 4, 1124–1130. http://dx.doi.org/10.1090/S0002-9939-1988-0943791-8 Google Scholar
[2] Bellow, A. and Calderón, A., A weak type inequality for convolution products. In: Harmonic Analysis and Partial Differential Equations. Chicago Lectures in Math. Univ. Chicago Press, Chicago, IL, 1999, pp. 41–48.Google Scholar
[3] Bellow, A., Jones, R. L., and Rosenblatt, J. M., Almost everywhere convergence of convolution products. Ergodic Theory Dynam. Systems 14(1994), no. 3, 415–432.Google Scholar
[4] Bellow, A., Jones, R. L., and Rosenblatt, J. M., Almost everywhere convergence of weighted averages. Math. Ann. 293(1992), no. 3, 399–426. http://dx.doi.org/10.1007/BF01444724 Google Scholar
[5] Losert, V., The strong sweeping out property for convolution powers. Ergodic Theory Dynam. Systems 21(2001), no. 1, 115–119.Google Scholar
[6] Losert, V., A remark on almost everywhere convegrence of convolution powers. Illinois J. Math. 43(1999), no. 3, 465–479.Google Scholar
[7] Ornstein, D., On the pointwise behavior of iterates of a self-adjoint operator. J. Math. Mech. 18(1968/1969), 473–477.Google Scholar
[8] Petersen, K., Ergodic Theory. Cambridge Studies in AdvancedMathematics 2. Cambridge University Press, Cambridge, 1983.Google Scholar
[9] Petrov, V. V., Sums of Independent Random Variables. Ergebnisse der Mathematik und ihrer Grenzgebiete 82. Springer-Verlag, New York, 1975.Google Scholar
[10] Rosenblatt, J. M., Universally bad sequences in ergodic theory. In: Almost Everywhere Convergence. II. Academic Press, Boston, MA, 1991, pp. 227–245.Google Scholar
[11] Rota, G. C., An “Alternierende Verfahren” for general positive operators. Bull. Amer. Math. Soc. 68(1962), 95–102. http://dx.doi.org/10.1090/S0002-9904-1962-10737-X Google Scholar