Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T18:58:09.905Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic Values of Entire Functions with Extremal Growth Orders: An Extension of a Theorem of Boxall and Jones

Published online by Cambridge University Press:  15 October 2019

Taboka Prince Chalebgwa
Taboka Prince Chalebgwa*
Affiliation:
Fields Institute, 222 College St, 3rd Floor, M5T 3J1, Toronto, Canada Department of Mathematical Sciences, Mathematics Division, Stellenbosch University, Private Bag X1, 7602 Matieland, South Africa Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

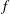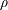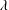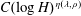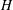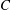Given an entire function $f$ of finite order $\unicode[STIX]{x1D70C}$ and positive lower order $\unicode[STIX]{x1D706}$, Boxall and Jones proved a bound of the form $C(\log H)^{\unicode[STIX]{x1D702}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D70C})}$ for the density of algebraic points of bounded degree and height at most $H$ on the restrictions to compact sets of the graph of $f$. The constant $C$ and exponent 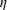$\unicode[STIX]{x1D702}$ are effectively computable from certain data associated with the function. In this followup note, using different measures of the growth of entire functions, we obtain similar bounds for other classes of functions to which the original theorem does not apply.

Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 3 , September 2020 , pp. 536 - 546
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This article was completed under the Fields-AIMS-Perimeter postdoctoral fellowship, provided by the Fields Institute for Research in Mathematical Sciences.

References

Berg, C., Pedersen, H., and Hayman, W., Logarithmic order and type of indeterminate moment problems. In: Difference equations, special functions and orthogonal polynomials. World Scientific Publishing, Hackensack, NJ, 2007. https://doi.org/10.1142/9789812770752_0005Google Scholar
Besson, E., Points rationnels de la fonction Gamma d’Euler. Arch Math. 103(2014), no. 1, 61–73. https://doi.org/10.1007/s00013-014-0661-1CrossRefGoogle Scholar
Bombieri, E. and Pila, J., The number of integral points on arcs and ovals. Duke Math. J. 59(1989), 237–275. https://doi.org/10.1215/S0012-7094-89-05915-2CrossRefGoogle Scholar
Boxall, G. and Jones, G., Rational values of entire functions of finite order. Int. Math. Res. Not. IMRN 2015, no. 22, 12251–12264. https://doi.org/10.1093/imrn/rnt239Google Scholar
Comte, G. and Yomdin, Y., Zeroes and rational points of analytic functions. Ann. Inst. Fourier 68(2018), no. 6, 2445–2476. https://doi.org/10.5802/aif.3213CrossRefGoogle Scholar
Hille, E., Analytic function theory, AMS Chelsea Publishing, Providence, RI, 1962.Google Scholar
Long, J. and Qin, Z., On the maximum term and central index of entire functions and their derivatives. J. Funct. Spaces 2018. https://doi.org/10.1155/2018/7028597Google Scholar
Masser, D., Rational values of the Riemann zeta function. J. Number Theory 131(2011), no. 11, 2037–2046. https://doi.org/10.1016/j.jnt.2011.03.013CrossRefGoogle Scholar
Pila, J., Geometric postulation of a smooth function and the number of rational points. Duke. Math. J. 63(1991), 449–463. https://doi.org/10.1215/S0012-7094-91-06320-9CrossRefGoogle Scholar
Surroca, A., Sur le nombre de points algébriques où une fonction analytique transcendante prend des valeurs algébriques. C. R. Math. Acad. Sci. 334(2002), no. 9, 721–725. https://doi.org/10.1016/s1631-073x(02)02335-xCrossRefGoogle Scholar
Waldschmidt, M., Diophantine approximation on linear algebraic groups. Grundlehren der Mathematischen Wissenschaften, 326, Springer-Verlag, Berlin, 2000. https://doi.org/org/10.1007/978-3-662-11569-5CrossRefGoogle Scholar
Yang, C.-C. and Yi, H.-X., Uniqueness theory of meromorphic functions, Springer, Netherlands, 2003.10.1007/978-94-017-3626-8CrossRefGoogle Scholar