Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T18:43:19.090Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic Homology For Real Hyperelliptic and Real Projective Ruled Surfaces

Published online by Cambridge University Press:  20 November 2018

Miguel A. Abánades
Miguel A. Abánades*
Affiliation:
Department of Mathematics and Statistics University of New Mexico Albuquerque, New Mexico 87131-1141 U.S.A., e-mail: [email protected]
*
Current address: IT Informática de Sistemas CES Felipe II C/ Capitan 39 Aranjuez 28300, Madrid Spain
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 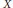$X$ be a reduced nonsingular quasiprojective scheme over 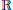$\mathbb{R}$ such that the set of real rational points 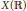$X\left( \mathbb{R} \right)$ is dense in 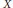$X$ and compact. Then 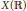$X\left( \mathbb{R} \right)$ is a real algebraic variety. Denote by 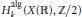$H_{k}^{a\lg }\left( X\left( \mathbb{R} \right),\,\mathbb{Z}/2 \right)$ the group of homology classes represented by Zariski closed 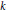$k$-dimensional subvarieties of 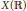$X\left( \mathbb{R} \right)$. In this note we show that 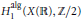$H_{1}^{a\lg }\left( X\left( \mathbb{R} \right),\,\mathbb{Z}/2 \right)$ is a proper subgroup of 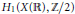${{H}_{1}}\left( X\left( \mathbb{R} \right),\,\mathbb{Z}/2 \right)$ for a nonorientable hyperelliptic surface 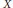$X$. We also determine all possible groups 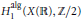$H_{1}^{a\lg }\left( X\left( \mathbb{R} \right),\,\mathbb{Z}/2 \right)$ for a real ruled surface 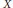$X$ in connection with the previously known description of all possible topological configurations of 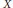$X$.

Keywords

14P0514P25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 3 , 01 September 2001 , pp. 257 - 265
Copyright
Copyright © Canadian Mathematical Society 2001

Footnotes

The author was partially supported by NSF Grant DMS-9503138.

References

[1] Bochnak, J., Coste, M. and Roy, M.-F., Real Algebraic Geometry. Ergebnisse der Math. 36, Berlin Heidelberg New York, Springer, 1998.Google Scholar
[2] Bochnak, J. and Kucharz, W., On homology classes represented by real algebraic varieties. Singularities Symposium Krakow 1996, Banach Center Publication, Institute of Mathematics Polish Academy of Sciences, Warschau, Polen, (1997), 7–22.Google Scholar
[3] Borel, A. et Haefliger, A., La classe d’homologie fondamentale d’un espace analytique. Bull. Soc.Math. France 89 (1961), 461–513.Google Scholar
[4] Fulton, W., Intersection Theory. Ergebnisse der Math. 2, Berlin, Heidelberg, New York, Springer, 1984.Google Scholar
[5] Huisman, J., Real abelian varieties with complex multiplication. Ph.D. thesis, Vrije Universiteit, Amsterdam, 1992.Google Scholar
[6] Kucharz, W., Algebraic equivalence and homology classes of real algebraic cycles. Math.Nachr. 180 (1996), 135–140.Google Scholar
[7] Mangolte, F., Cycles algebriques sur les surfaces K3 réelles. Math. Z. 225 (1997), 559–576.Google Scholar
[8] Mangolte, F. and van Hamel, J., Algebraic cycles on real Enriques surfaces. Comp. Math. 110 (1998), 215–237.Google Scholar
[9] Silhol, R., Cohomology de Galois et cohomologie des variétés algebriques réelles: application aux surfaces rationnelles. Bull. Soc.Math. France 115 (1987), 107–125.Google Scholar
[10] Silhol, R., Real algebraic surfaces. LectureNotes in Math., 1392, Springer-Verlag, Berlin, Heidelberg, New York, 1989.Google Scholar
[11] Witt, E., Zerlegung reeller algebraisher Funktionen in Quadrate, Schiefkörper über reellem Funktionenkörpern. J. Reine Angew.Math. 171 (1934), 4–11.Google Scholar