Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T16:35:18.578Z Has data issue: false hasContentIssue false
  • English
  • Français

A Vanishing Theorem for the Twisted Normal Bundle of Curves in 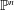$\mathbb{P}^{n}$, 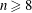$n\geqslant 8$

Part of: Curves

Published online by Cambridge University Press:  30 August 2019

E. Ballico
E. Ballico*
Affiliation:
Department of Mathematics, University of Trento, 38123Povo (TN), Italy Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the existence of a smooth and non-degenerate curve 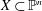$X\subset \mathbb{P}^{n}$, 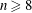$n\geqslant 8$, with 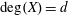$\deg (X)=d$, 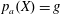$p_{a}(X)=g$, 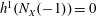$h^{1}(N_{X}(-1))=0$, and general moduli for all 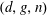$(d,g,n)$ such that 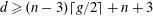$d\geqslant (n-3)\lceil g/2\rceil +n+3$. It was proved by C. Walter that, for 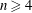$n\geqslant 4$, the inequality 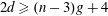$2d\geqslant (n-3)g+4$ is a necessary condition for the existence of a curve with 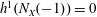$h^{1}(N_{X}(-1))=0$.

Keywords

projective curvenormal bundletwisted normal bundle

MSC classification

Primary: 14H50: Plane and space curves
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 1 , March 2020 , pp. 1 - 5
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was partially supported by MIUR and GNSAGA of INdAM (Italy).

References

Atanasov, A., Interpolation and vector bundles on curves. arxiv:1404.4892Google Scholar
Atanasov, A., Larson, E., and Yang, D., Interpolation for normal bundles of general curves. arxiv:1509.01724Google Scholar
Ballico, E. and Ellia, P., Bonnes petites composantes des schémas de Hilbert de courbes lisses de ℙn. C. R. Acad. Sci. Paris Sér. I Math. 306(1988), no. 4, 187–190.Google Scholar
Ellingsrud, G. and Hirschowitz, A., Sur le fibré normal des courbes gauches. C. R. Acad. Sci. Paris Sér. I Math. 299(1984), no. 7, 245–248.Google Scholar
Hartshorne, R. and Hirschowitz, A., Smoothing algebraic space curves. In: Algebraic geometry. Lecture Notes in Math., 1124, Springer, Berlin, 1985, pp. 98–131. https://doi.org/10.1007/BFb0074998Google Scholar
Larson, E., Interpolation for restricted tangent bundles of general curves. Algebra Number Theory 10(2016), no. 4, 931–938. https://doi.org/10.2140/ant.2016.10.931Google Scholar
Larson, E., Constructing reducible Brill–Noether curves. arxiv:1603.02301Google Scholar
Larson, E., The generality of a section of a curve. arxiv:1605.06185Google Scholar
Larson, E., Interpolation with bounded error. arxiv:1711.01729Google Scholar
Larson, E. and Vogt, I., Interpolation for Brill–Noether curve in ℙ4. arxiv:1708.00028Google Scholar
Perrin, D., Courbes passant par m points généraux de P3. Mém. Math. France, Mem. no. 28/29, 1987.Google Scholar
Ran, Z., Normal bundles of rational curves in projective spaces. Asian J. Math. 11(2007), no. 4, 567–608. https://doi.org/10.4310/AJM.2007.v11.n4.a3Google Scholar
Sacchiero, G., Normal bundle of rational curves in projective space. Ann. Univ. Ferrara Sez. VII (N.S.) 26(1981), 33–40.Google Scholar
Sernesi, E., On the existence of certain families of curves. Invent. Math. 75(1984), 25–57. https://doi.org/10.1007/BF01403088Google Scholar
Vogt, I., Interpolation for Brill-Noether space curves. Manuscripta Math. 156(2018), 137–147. https://doi.org/10.1007/s00229-017-0961-4Google Scholar
Walter, C., Hyperplane sections of arithmetically Cohen–Macaulay curves. Proc. Amer. Math. Soc. 123(1995), no. 9, 2651–2656.Google Scholar