Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-05T23:05:01.556Z Has data issue: false hasContentIssue false
  • English
  • Français

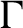Uniform property $\Gamma $ for certain $\mathrm {C^*}$-algebras

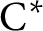Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  10 January 2022

Qingzhai Fan  and
Shan Zhang
Qingzhai Fan*
Affiliation:
Department of Mathematics, Shanghai Maritime University, Shanghai 201306, China College of Education, Shanghai Jian Qiao University, Shanghai 201306, China
Shan Zhang
Affiliation:
Department of Mathematics, Shanghai Maritime University, Shanghai 201306, China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

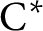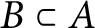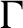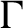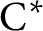In this paper, let A be an infinite-dimensional stably finite unital simple separable $\mathrm {C^*}$ -algebra. Let $B\subset A$ be a centrally large subalgebra in A such that B has uniform property $\Gamma $ . Then we prove that A has uniform property $\Gamma $ . 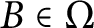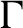Let $\Omega $ be a class of stably finite unital $\mathrm {C^*}$ -algebras such that for any $B\in \Omega $ , B has uniform property $\Gamma $ . 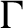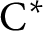Then we show that A has uniform property $\Gamma $ for any simple unital $\mathrm {C^*}$ -algebra 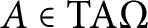$A\in \rm {TA}\Omega $ .

Keywords

C*-algebrastracial approximationCuntz semigroup

MSC classification

Primary: 46L35: Classifications of $C^*$-algebras
Secondary: 46L05: General theory of $C^*$-algebras 46L80: $K$-theory and operator algebras (including cyclic theory)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 4 , December 2022 , pp. 1063 - 1070
Check for updates
Copyright
© Canadian Mathematical Society, 2022

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Archey, D. and Phillips, N. C., Permanence of stable rank one for centrally large subalgebra and crossed products by minimal homeomorphisms. J. Operator Theory 83(2020), 353–389.CrossRefGoogle Scholar
Bosa, J., Brown, N. P., Sato, Y., Tikuisis, A., White, S., and Winter, W., Covering dimension of $\ {\mathrm{C}}^{\ast }$ -algebras and 2-coloured classification, Mem. Amer. Math. Soc. 257(2019), no. 1233, vii+97 pp.Google Scholar
Castillejos, J., Evington, S., Tikuisis, A., and White, S., Uniform property Γ. Int. Math. Res. Not. IMRN. Published online 13 February 2021.https://doi.org/10.1093/imrn/rnaa282 Google Scholar
Castillejos, J., Evington, S., Tikuisis, A., White, S., and Winter, W., Nuclear dimension of simple $\ {\mathrm{C}}^{\ast }$ -algebras. Invent. Math. 224(2021), 245–290.CrossRefGoogle Scholar
Elliott, G. A., On the classification of inductive limits of sequences of semisimple finite dimensional algebras. J. Algebra 38(1976), 29–44.CrossRefGoogle Scholar
Elliott, G. A., Fan, Q., and Fang, X., Certain properties of tracial approximation $\ {\mathrm{C}}^{\ast }$ -algebras, C. R. Math. Rep. Acad. Sci. Canada 40 (2018), 104–133.Google Scholar
Elliott, G. A. and Niu, Z., On tracial approximation. J. Funct. Anal. 254(2008), 396–440.CrossRefGoogle Scholar
Elliott, G. A. and Toms, A., Regularity properties in the classification program for separable amenable $\ {\mathrm{C}}^{\ast }$ -algebras. Bull. Amer. Math. Soc. 45(2008), 229–245.CrossRefGoogle Scholar
Fan, Q., Certain Cuntz semigroup properties of certain crossed product $\ {\mathrm{C}}^{\ast }$ -algebra. Acta Math. Sin. (Engl. Ser.) 36(2020), 337–362.CrossRefGoogle Scholar
Fan, Q. and Fang, X., Crossed products by finite group actions with a certain tracial Rokhlin property. Acta Math. Sci. 38(2018), 829–842.CrossRefGoogle Scholar
Kerr, D. and Szabó, G., Almost finiteness and the small boundary property. Comm. Math. Phys. 374(2020), 1–31.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M., Central sequence $\ {\mathrm{C}}^{\ast }$ -algebras and tensorial absorption of the Jiang–Su algebra. J. Reine Angew. Math. 695(2014), 175–214.CrossRefGoogle Scholar
Lin, H., The tracial topological rank of  $\ {\mathrm{C}}^{\ast }$ -algebras. Proc. Lond. Math. Soc. 83(2001), 199–234.CrossRefGoogle Scholar
Lin, H., An introduction to the classification of amenable $\ {\mathrm{C}}^{\ast }$ -algebras, World Scientific, Hackensack–London–Singapore–Hong Kong, 2001.Google Scholar
Phillips, N. C., The tracial Rokhlin property for actions of finite groups on $\ {\mathrm{C}}^{\ast }$ -algebras. Amer. J. Math. 133(2011), 581–636.CrossRefGoogle Scholar
Phillips, N. C., Large subalgebras. Preprint, 2014.arXiv:1408.5546 Google Scholar
Toms, A., White, W., and Winter, W., $\mathbf{\mathcal{Z}}$ -stability and finite dimensional tracial boundaries. Int. Math. Res. Not. IMRN 10(2015), 2702–2727.Google Scholar