Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-26T00:48:02.712Z Has data issue: false hasContentIssue false
  • English
  • Français

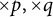A tracial characterization of Furstenberg’s $\times p,\times q$ conjecture

Part of: Selfadjoint operator algebras Ergodic theory

Published online by Cambridge University Press:  06 September 2023

Chris Bruce Open the ORCID record for Chris Bruce [Opens in a new window]  and
Eduardo Scarparo Open the ORCID record for Eduardo Scarparo [Opens in a new window]
Chris Bruce*
Affiliation:
School of Mathematics and Statistics, University of Glasgow, University Place, Glasgow G12 8QQ, United Kingdom
Eduardo Scarparo
Affiliation:
Center for Engineering, Federal University of Pelotas, Pelotas, Brazil e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate almost minimal actions of abelian groups and their crossed products. As an application, given multiplicatively independent integers p and q, we show that Furstenberg’s 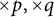$\times p,\times q$ conjecture holds if and only if the canonical trace is the only faithful extreme tracial state on the 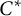$C^*$-algebra of the group 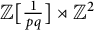$\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2$. We also compute the primitive ideal space and K-theory of 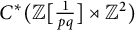$C^*(\mathbb {Z}[\frac {1}{pq}]\rtimes \mathbb {Z}^2)$.

Keywords

Furstenberg conjecturetracial statesprimitive idealsK-theory

MSC classification

Primary: 37A55: Relations with the theory of $C^*$-algebras 46L05: General theory of $C^*$-algebras
Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 1 , March 2024 , pp. 244 - 256
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alekseev, V., (Non)-uniqueness of ${\mathrm{C}}^{\ast }$ -norms on group rings of amenable groups . Oberwolfach Rep. 37(2019), 2229–2294.Google Scholar
Becker, O., Lubotzky, A., and Thom, A., Stability and invariant random subgroups . Duke Math. J. 168(2019), no. 12, 2207–2234.CrossRefGoogle Scholar
Bekka, B. and de la Harpe, P., Unitary representations of groups, duals, and characters, Mathematical Surveys and Monographs, 250, American Mathematical Society, Providence, RI, 2020.CrossRefGoogle Scholar
Berend, D., Multi-invariant sets on tori . Trans. Amer. Math. Soc. 280(1983), no. 2, 509–532.CrossRefGoogle Scholar
Berend, D., Multi-invariant sets on compact abelian groups . Trans. Amer. Math. Soc. 286(1984), no. 2, 505–535.CrossRefGoogle Scholar
Breuillard, E., Kalantar, M., Kennedy, M., and Ozawa, N., ${\mathrm{C}}^{\ast }$ -simplicity and the unique trace property for discrete groups . Publ. Math. Inst. Hautes Etudes Sci. 126(2017), 35–71.CrossRefGoogle Scholar
Brown, N. P. and Ozawa, N., C* -algebras and finite-dimensional approximations , Graduate Studies in Mathematics, 88, American Mathematical Society, Providence, RI, 2008.CrossRefGoogle Scholar
Furstenberg, H., Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation . Math. Syst. Theory 1(1967), 1–49.CrossRefGoogle Scholar
Grigorchuk, R., Musat, M., and Rørdam, M., Just-infinite ${\mathrm{C}}^{\ast }$ -algebras . Comment. Math. Helv. 93(2018), no. 1, 157–201.CrossRefGoogle Scholar
Huang, H. and Wu, J., Ergodic invariant states and irreducible representations of crossed product ${\mathrm{C}}^{\ast }$ -algebras . J. Operator Theory 78(2017), no. 1, 159–172.CrossRefGoogle Scholar
Kawamura, S., Takemoto, H., and Tomiyama, J., State extensions in transformation group ${C}^{\ast }$ -algebras . Acta Sci. Math. (Szeged) 54 (1990), nos. 1–2, 191–200.Google Scholar
Laca, M. and Warren, J. M., Phase transitions on ${\mathrm{C}}^{\ast }$ -algebras arising from number fields and the generalized Furstenberg conjecture . J. Operator Theory 83(2020), no. 1, 73–93.CrossRefGoogle Scholar
Lindenstrauss, E., Rigidity of multiparameter actions . Israel J. Math. 149(2005), 199–226.CrossRefGoogle Scholar
Murphy, G. J., C* -algebras and operator theory , Academic Press, Inc., Boston, MA, 1990.Google Scholar
Neshveyev, S., KMS states on the ${\mathrm{C}}^{\ast }$ -algebras of non-principal groupoids . J. Operator Theory 70(2013), no. 2, 513–530.CrossRefGoogle Scholar
Pimsner, M. and Voiculescu, D., Exact sequences for K-groups and Ext-groups of certain cross-product ${\mathrm{C}}^{\ast }$ -algebras . J. Operator Theory 4(1980), no. 1, 93–118.Google Scholar
Pooya, S. and Valette, A., K-theory for the ${C}^{\ast }$ -algebras of the solvable Baumslag–Solitar groups . Glasg. Math. J. 60(2018), no. 2, 481–486.CrossRefGoogle Scholar
Rørdam, M., Just-infinite ${C}^{\ast }$ -algebras and their invariants . Int. Math. Res. Not. IMRN 12(2019), 3621–3645.CrossRefGoogle Scholar
Scarparo, E., A torsion-free algebraically ${\mathrm{C}}^{\ast }$ -unique group . Rocky Mountain J. Math. 50(2020), no. 5, 1813–1815.CrossRefGoogle Scholar
Schmidt, K., Dynamical systems of algebraic origin, Progress in Mathematics, 128, Birkhauser, Basel, 1995.Google Scholar
Vaes, S., Faithful extreme traces on group ${C}^{\ast }$ -algebras. https://mathoverflow.net/q/436810.Google Scholar
Williams, D. P., The topology on the primitive ideal space of transformation group ${\mathrm{C}}^{\ast }$ -algebras and C.C.R. transformation group ${\mathrm{C}}^{\ast }$ -algebras . Trans. Amer. Math. Soc. 266(1981), no. 2, 335–359.Google Scholar