For any prime p, let 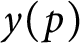$y(p)$ denote the smallest integer y such that every reduced residue class (mod p) is represented by the product of some subset of $\{1,\dots ,y\}$ . It is easy to see that 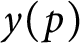$y(p)$ is at least as large as the smallest quadratic nonresidue (mod p); we prove that 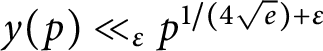$y(p) \ll _\varepsilon p^{1/(4 \sqrt e)+\varepsilon }$ , thus strengthening Burgess’ classical result. 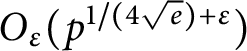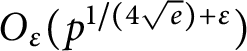This result is of intermediate strength between two other results, namely Burthe’s proof that the multiplicative group (mod p) is generated by the integers up to $O_\varepsilon (p^{1/(4 \sqrt e)+\varepsilon })$ , and Munsch and Shparlinski’s result that every reduced residue class (mod p) is represented by the product of some subset of the primes up to $O_\varepsilon (p^{1/(4 \sqrt e)+\varepsilon })$ . Unlike the latter result, our proof is elementary and similar in structure to Burgess’ proof for the least quadratic nonresidue.