Hostname: page-component-5cf477f64f-tgq86 Total loading time: 0 Render date: 2025-04-02T07:39:07.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Ricci Solitons on Almost Co-Kähler Manifolds

Part of: Global differential geometry Symplectic geometry, contact geometry

Published online by Cambridge University Press:  07 December 2018

Yaning Wang
Yaning Wang*
Affiliation:
School of Mathematics and Information Sciences, Henan Normal University, Xinxiang 453007, Henan, P. R. China Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

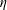In this paper, we prove that if an almost co-Kähler manifold of dimension greater than three satisfying $\unicode[STIX]{x1D702}$-Einstein condition with constant coefficients is a Ricci soliton with potential vector field being of constant length, then either the manifold is Einstein or the Reeb vector field is parallel. Let 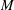$M$ be a non-co-Kähler almost co-Kähler 3-manifold such that the Reeb vector field 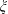$\unicode[STIX]{x1D709}$ is an eigenvector field of the Ricci operator. If 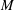$M$ is a Ricci soliton with transversal potential vector field, then it is locally isometric to Lie group 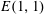$E(1,1)$ of rigid motions of the Minkowski 2-space.

Keywords

almost co-Kähler manifoldRicci soliton𝜂-EinsteinLie group

MSC classification

Primary: 53D15: Almost contact and almost symplectic manifolds
Secondary: 53C25: Special Riemannian manifolds (Einstein, Sasakian, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 4 , December 2019 , pp. 912 - 922
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work was supported by Youth Science Foundation of Henan Normal University (No. 2014QK01).

References

Blair, D. E., The theory of quasi-Sasakian structures . J. Differential Geometry 1(1967), 331–345.Google Scholar
Blair, D. E., Riemannian geometry of contact and symplectic manifolds . Progress in Mathematics, 203, Birkhäuser, Boston, 2010. https://doi.org/10.1007/978-0-8176-4959-3 Google Scholar
Cappelletti-Montano, B., Nicola, A. D., and Yudin, I., A survey on cosymplectic geometry . Rev. Math. Phys. 25(2013), 1343002, 55 pp. https://doi.org/10.1142/S0129055X13430022 Google Scholar
Conti, D. and Fernández, M., Einstein almost cokähler manifolds . Math. Nachr. 289(2016), 1396–1407. https://doi.org/10.1002/mana.201400412 Google Scholar
Cho, J. T., Almost contact 3-manifolds and Ricci solitons . Int. J. Geom. Methods Mod. Phys. 10(2013), 1220022, 7 pp. https://doi.org/10.1142/S0219887812200228 Google Scholar
Hamilton, R. S., Three-manifolds with positive Ricci curvature . J. Differ. Geom. 17(1982), 255–306. https://doi.org/10.4310/jdg/1214436922 Google Scholar
Hamilton, R. S., The Ricci flow on surfaces . Contemp. Math., 71, American Mathematicl Society, Providence, RI, 1988. https://doi.org/10.1090/conm/071/954419 Google Scholar
Lee, S. D., Byung, H. K., and Choi, J. H., On a classification of warped product spaces with gradient Ricci solitons . Korean J. Math. 24(2016), 627–636. https://doi.org/10.11568/kjm.2016.24.4.627 Google Scholar
Li, H., Topology of co-symplectic/co-Kähler manifolds . Asian J. Math. 12(2008), 527–544. https://doi.org/10.4310/AJM.2008.v12.n4.a7 Google Scholar
Montano, B. C. and Pastore, A. M., Einstein-like conditions and cosymplectic geometry . J. Adv. Math. Stud. 3(2010), 27–40.Google Scholar
Olszak, Z., On almost cosymplectic manifolds . Kodai Math. J. 4(1981), 239–250.Google Scholar
Olszak, Z., Locally conformal almost cosymplectic manifolds . Colloq. Math. 57(1989), 73–87. https://doi.org/10.4064/cm-57-1-73-87 Google Scholar
Oguro, T. and Sekigawa, K., Almost Kähler structures on the Riemannian product of a 3-dimensional hyperbolic space and a real line . Tsukuba J. Math. 20(1996), 151–161. https://doi.org/10.21099/tkbjm/1496162985 Google Scholar
Perelman, G., The entropy formula for the Ricci flow and its geometric applications. 2012. arxiv:math/0211159 Google Scholar
Perrone, D., Minimal Reeb vector fields on almost cosymplectic manifolds . Kodai Math. J. 36(2013), 258–274. https://doi.org/10.2996/kmj/1372337517 Google Scholar
Wang, W., A class of three dimensional almost co-Kähler manifolds . Palest. J. Math. 6(2017), 111–118.Google Scholar
Wang, W. and Liu, X., Three-dimensional almost co-Kähler manifolds with harmonic Reeb vector field . Rev. Un. Mat. Argentina 58(2017), 307–317.Google Scholar
Wang, Y., A generalization of the Goldberg conjecture for co-Kähler manifolds . Mediterr. J. Math. 13(2016), 2679–2690. https://doi.org/10.1007/s00009-015-0646-8 Google Scholar
Wang, Y., Ricci solitons on 3-dimensional cosymplectic manifolds . Math. Slovaca 67(2017), 979–984. https://doi.org/10.1515/ms-2017-0026 Google Scholar
Yano, K., Integral formulas in Riemannian geometry . Pure and Applied Mathematics, No. 1, Marcel Dekker, New York, 1970.Google Scholar