Article contents
Revisiting G-Dedekind domains
Published online by Cambridge University Press: 20 December 2021
Abstract
Let R be an integral domain with
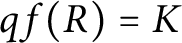 $qf(R)=K$
, and let
$qf(R)=K$
, and let
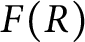 $F(R)$
be the set of nonzero fractional ideals of R. Call R a dually compact domain (DCD) if, for each
$F(R)$
be the set of nonzero fractional ideals of R. Call R a dually compact domain (DCD) if, for each
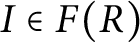 $I\in F(R)$
, the ideal
$I\in F(R)$
, the ideal
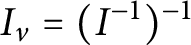 $I_{v}=(I^{-1})^{-1}$
is a finite intersection of principal fractional ideals. We characterize DCDs and show that the class of DCDs properly contains various classes of integral domains, such as Noetherian, Mori, and Krull domains. In addition, we show that a Schreier DCD is a greatest common divisor (GCD) (Greatest Common Divisor) domain with the property that, for each
$I_{v}=(I^{-1})^{-1}$
is a finite intersection of principal fractional ideals. We characterize DCDs and show that the class of DCDs properly contains various classes of integral domains, such as Noetherian, Mori, and Krull domains. In addition, we show that a Schreier DCD is a greatest common divisor (GCD) (Greatest Common Divisor) domain with the property that, for each
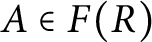 $A\in F(R)$
, the ideal
$A\in F(R)$
, the ideal
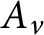 $A_{v}$
is principal. We show that a domain R is G-Dedekind (i.e., has the property that
$A_{v}$
is principal. We show that a domain R is G-Dedekind (i.e., has the property that
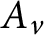 $A_{v}$
is invertible for each
$A_{v}$
is invertible for each
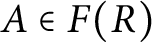 $A\in F(R)$
) if and only if R is a DCD satisfying the property
$A\in F(R)$
) if and only if R is a DCD satisfying the property
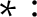 $\ast :$
For all pairs of subsets
$\ast :$
For all pairs of subsets
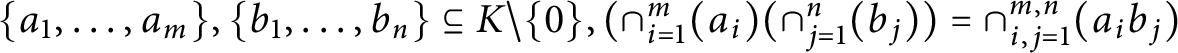 $\{a_{1},\ldots ,a_{m}\},\{b_{1},\ldots ,b_{n}\}\subseteq K\backslash \{0\}, (\cap _{i=1}^{m}(a_{i})(\cap _{j=1}^{n}(b_{j}))=\cap _{i,j=1}^{m,n}(a_{i}b_{j})$
. We discuss what the appropriate names for G-Dedekind domains and related notions should be. We also make some observations about how the DCDs behave under localizations and polynomial ring extensions.
$\{a_{1},\ldots ,a_{m}\},\{b_{1},\ldots ,b_{n}\}\subseteq K\backslash \{0\}, (\cap _{i=1}^{m}(a_{i})(\cap _{j=1}^{n}(b_{j}))=\cap _{i,j=1}^{m,n}(a_{i}b_{j})$
. We discuss what the appropriate names for G-Dedekind domains and related notions should be. We also make some observations about how the DCDs behave under localizations and polynomial ring extensions.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society, 2021
Footnotes
Dedicated to fairness
References
- 1
- Cited by



