Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T15:27:05.859Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative vertex asphericity

Part of: Special aspects of infinite or finite groups Low-dimensional topology

Published online by Cambridge University Press:  16 June 2020

Jens Harlander  and
Stephan Rosebrock
Jens Harlander
Affiliation:
Department of Mathematics, Boise State University, Boise, ID83725-1555, USA e-mail: [email protected]
Stephan Rosebrock*
Affiliation:
Pädagogische Hochschule Karlsruhe, Bismarckstr. 10, 76133Karlsruhe, Germany
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Diagrammatic reducibility DR and its generalization, vertex asphericity VA, are combinatorial tools developed for detecting asphericity of a 2-complex. Here we present tests for a relative version of VA that apply to pairs of 2-complexes 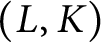$(L,K)$ , where K is a subcomplex of L. We show that a relative weight test holds for injective labeled oriented trees, implying that they are VA and hence aspherical. This strengthens a result obtained by the authors in 2017 and simplifies the original proof.

Keywords

Diagrammatic reducibilityasphericity2-complexweight testrelative asphericity

MSC classification

Primary: 57M20: Two-dimensional complexes
Secondary: 20F05: Generators, relations, and presentations 20F06: Cancellation theory; application of van Kampen diagrams 20F65: Geometric group theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 2 , June 2021 , pp. 292 - 305
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barmak, J. and Minian, G., A new test for asphericity and diagrammatic reducibility of group presentations. Proc. R. Soc. Edinb. Sec. A: Math. 150(2020), 871–895.CrossRefGoogle Scholar
Blufstein, M. A. and Minian, E. G., Strictly systolic angled complexes and hyperbolicity of one-relator groups. Preprint, 2019. https://arxiv.org/abs/1907.06738 Google Scholar
Bogley, W. and Pride, S., Aspherical relative presentations . Proc. Edinb. Math. Society 35(1992), 1–39.CrossRefGoogle Scholar
Bogley, W., Edjvet, M. and Williams, G., Aspherical relative presentations all over again. In: Campbell, C. M., W. Parker, C., Quick, M. R., and Robertson, E. F. (eds.), Groups St Andrews 2017 in Birmingham, London Math. Soc. Lecture Note Series, Cambridge University Press, Cambridge, UK (2019), pp. 169–199.CrossRefGoogle Scholar
Collins, D. J. and Huebschmann, J., Spherical diagrams and identities among relations. Math. Ann. 261(1982), 155–183.CrossRefGoogle Scholar
Corson, J. M. and Trace, B., Geometry and algebra of nonspherical 2-complexes. J. London Math. Soc. 54(1996), 180–198.CrossRefGoogle Scholar
Corson, J. M. and Trace, B., Diagrammatically reducible complexes and Haken manifolds. J. Austral. Math. Soc. (Series A) 69(2000), 116–126.CrossRefGoogle Scholar
Gersten, S. M., Reducible diagrams and equations over groups. In: Gersten, S. M. (ed.), Essays in Group Theory, MSRI Publications 8(1987), pp. 15–73.CrossRefGoogle Scholar
Harlander, J. and Rosebrock, S., Injective labelled oriented trees are aspherical. Mathematische Zeitschrift 287 (1)(2017), 199–214.CrossRefGoogle Scholar
Harlander, J., Rosebrock, S., Directed diagrammatic reducibility. Topol. Appl. (2020), to appear.CrossRefGoogle Scholar
Huck, G. and Rosebrock, S., Weight tests and hyperbolic groups. In: Duncan, A., Gilbert, N., and Howie, J. (eds.), Combinatorial and Geometric Group Theory (Edinburgh, 1993), London Math. Soc. Lecture Notes Series 204, Cambridge University Press, Cambridge, UK (1995), pp. 174–183.Google Scholar
Huck, G. and Rosebrock, S., Aspherical labeled oriented trees and knots. Proc. Edinb. Math. Soc. 44(2001), 285–294.CrossRefGoogle Scholar
Rosebrock, S., Labelled oriented trees and the Whitehead conjecture. In: Metzler, W. and Rosebrock, S. (eds.), Advances in Two-Dimensional Homotopy and Combinatorial Group Theory, London Math. Soc. Lect. Notes Series 446, Cambridge University Press, Cambridge, UK (2018), pp. 72–97.Google Scholar
Sieradski, A., A coloring test for asphericity. Quart. J. Math. Oxford (2) 34(1983), 97–106.CrossRefGoogle Scholar
Wise, D., Sectional curvature, compact cores, and local-quasiconvexity. Geom. Funct. Anal. 14(2004), 433–468. CrossRefGoogle Scholar