Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T14:44:19.448Z Has data issue: false hasContentIssue false
  • English
  • Français

The Modularity of Special Cycles on Orthogonal Shimura Varieties over Totally Real Fields under the Beilinson–Bloch Conjecture

Part of: Arithmetic algebraic geometry Cycles and subschemes Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  30 March 2020

Yota Maeda
Yota Maeda*
Affiliation:
Department of Mathematics, Faculty of Science, Kyoto University, Kyoto606-8502, Japan
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study special cycles on a Shimura variety of orthogonal type over a totally real field of degree d associated with a quadratic form in 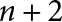$n+2$ variables whose signature is 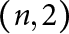$(n,2)$ at e real places and 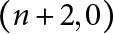$(n+2,0)$ at the remaining 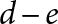$d-e$ real places for 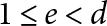$1\leq e <d$. Recently, these cycles were constructed by Kudla and Rosu–Yott, and they proved that the generating series of special cycles in the cohomology group is a Hilbert-Siegel modular form of half integral weight. We prove that, assuming the Beilinson–Bloch conjecture on the injectivity of the higher Abel–Jacobi map, the generating series of special cycles of codimension er in the Chow group is a Hilbert–Siegel modular form of genus r and weight 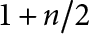$1+n/2$. Our result is a generalization of Kudla’s modularity conjecture, solved by Yuan–Zhang–Zhang unconditionally when 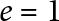$e=1$.

Keywords

Shimura varietiesmodular formsalgebraic cycles

MSC classification

Primary: 11G18: Arithmetic aspects of modular and Shimura varieties
Secondary: 11F46: Siegel modular groups; Siegel and Hilbert-Siegel modular and automorphic forms 14C17: Intersection theory, characteristic classes, intersection multiplicities
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 1 , March 2021 , pp. 39 - 53
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beilinson, A., Height pairing between algebraic cycles. K-theory, Arithmetic and Geometry (Moscow, 1984-1986), 1–25, Lecture Notes in Math., 1289, Springer, Berlin, 1987.Google Scholar
Bergeron, N., Millson, J., and Moeglin, C., Hodge type theorems for arithmetic manifolds associated to orthogonal groups. Int. Math. Res. Not. IMRN 2017(2017), no. 15, 4495–4624.Google Scholar
Borel, A. and Wallach, N., Continuous cohomology, discrete subgroups, and representations of reductive groups. Mathematical Surveys and Monographs. 67. American Mathematical Society, Providence, RI, 2000.CrossRefGoogle Scholar
Borcherds, R., Automorphic forms with singularities on Grassmannians. Invent. Math. 132 (1998), no. 3, 491–562.CrossRefGoogle Scholar
Borcherds, R., The Gross-Kohnen-Zagier theorem in higher dimensions. Duke Math. J. 97(1999), no. 2, 219–233.CrossRefGoogle Scholar
Bruinier, J., Westerholt-Raum, M., Kudla’s modularity conjecture and formal Fourier-Jacobi series. Forum Math. Pi 3(2015), e7, 30 pp.CrossRefGoogle Scholar
Gorodnik, A., Maucourant, F., and Oh, H., Manin’s and Peyre’s conjectures on rational points and adelic mixing. Ann. Sci. Éc. Norm. Supér. (4) 41(2008), no. 3, 383–435.Google Scholar
Gourevitch, D. and Kemarsky, A., Irreducible representations of product of real reductive groups. J. Lie Theory 23(2013), no. 4, 1005–1010.Google Scholar
Gross, B., Kohnen, W., and Zagier, D., Heegner points and derivatives of L-series. II. Math. Ann. 278 (1987), no. 1-4, 497–562.CrossRefGoogle Scholar
Hirzebruch, F. and Zagier, D., Intersection numbers of curves on Hilbert modular surfaces and modular forms of Nebentypus. Invent. Math. 36 (1976), 57–113.CrossRefGoogle Scholar
Jannsen, U., Motivic sheaves and filtrations on Chow groups. Motives (Seattle, WA, 1991), 245–302, Proc. Sympos. Pure Math., 55, Part 1, Amer. Math. Soc., Providence, RI, 1994.Google Scholar
Kudla, S. and Millson, J., Intersection numbers of cycles on locally symmetric spaces and Fourier coefficients of holomorphic modular forms in several complex variables. Inst. Hautes Études Sci. Publ. Math. No. 71 (1990), 121–172.CrossRefGoogle Scholar
Kudla, S., Algebraic cycles on Shimura varieties of orthogonal type. Duke Math. J. 86 (1997), no. 1, 39–78.CrossRefGoogle Scholar
Kudla, S., Central derivatives of Eisenstein series and height pairings. Ann. of Math. (2) 146 (1997), no. 3, 545–646.CrossRefGoogle Scholar
Kudla, S., Integrals of Borcherds forms. Compositio Math. 137 (2003), no. 3, 293–349.CrossRefGoogle Scholar
Kudla, S., Special cycles and derivatives of Eisenstein series. Heegner points and Rankin L-series, 243–270. Math. Sci. Res. Inst. Publ., 49, Cambridge Univ. Press, Cambridge, 2004.Google Scholar
Kudla, S., Remarks on generating series for special cycles. arXiv:1908.08390.Google Scholar
Kumaresan, S., On the canonical k-types in the irreducible unitary g-modules with non-zero relative cohomology. Invent. Math. 59 (1980), no. 1, 1–11.CrossRefGoogle Scholar
Rosu, E. and Yott, D., Generating series of a new class of orthogonal Shimura varieties. arXiv:1812.05183.Google Scholar
Vogan, D. and Zuckerman, G., Unitary representations with nonzero cohomology. Compositio Math. 53 (1984), no. 1, 51–90.Google Scholar
Warner, G., Harmonic analysis on semi-simple Lie groups. I, Die Grundlehren der mathematischen Wissenschaften, Band 188. Springer-Verlag, New York-Heidelberg, 1972.Google Scholar
Yuan, X., Zhang, S.-W., and Zhang, W., The Gross-Kohnen-Zagier theorem over totally real fields. Compositio Math. 145 (2009), no. 5, 1147–1162.CrossRefGoogle Scholar
Zhang, W., Modularity of generating functions of special cycles on Shimura varieties. Ph. D Thesis, Columbia University, 2009, 48 pp.Google Scholar