Hostname: page-component-f554764f5-c4bhq Total loading time: 0 Render date: 2025-04-19T01:48:48.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Hilbert’s 10th problem via Mordell curves

Part of: Diophantine equations Arithmetic algebraic geometry Number theory: Connections with logic

Published online by Cambridge University Press:  26 February 2025

Somnath Jha ,
Debanjana Kundu Open the ORCID record for Debanjana Kundu [Opens in a new window]  and
Dipramit Majumdar Open the ORCID record for Dipramit Majumdar [Opens in a new window]
Somnath Jha*
Affiliation:
Department of Mathematical and Statistics, IIT Kanpur, Kanpur, India
Debanjana Kundu
Affiliation:
Department of Mathematical and Statistical Sciences, UTRGV, 1201 W University Dr., Edinburg, TX 78539, United States e-mail: [email protected]
Dipramit Majumdar
Affiliation:
Department of Mathematics, IIT Madras, Chennai, India e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for 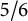$5/6$-th of all primes p, Hilbert’s 10th problem is unsolvable for the ring of integers of 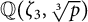$\mathbb {Q}(\zeta _3, \sqrt [3]{p})$. We also show that there is an infinite set S of square-free integers such that Hilbert’s 10th problem is unsolvable over the ring of integers of 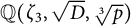$\mathbb {Q}(\zeta _3, \sqrt {D}, \sqrt [3]{p})$ for every 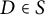$D \in S$ and for every prime 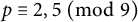$p \equiv 2, 5\ \pmod 9$. We use the CM elliptic curves 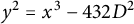$y^2=x^3-432 D^2$ associated with the cube-sum problem, with D varying in suitable congruence class, in our proof.

Keywords

Hilbert’s 10th Problemcube-sum problemelliptic curvescubic twists

MSC classification

Primary: 11G05: Elliptic curves over global fields
Secondary: 11U05: Decidability 11D25: Cubic and quartic equations
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alpöge, L., Bhargava, M., Ho, W., and Shnidman, A., Rank stability in quadratic extensions and Hilbert’s tenth problem for the ring of integers of a number field. Preprint, 2025. https://arxiv.org/abs/2501.18774 Google Scholar
Alpöge, L., Bhargava, M., and Shnidman, A. (with an appendix by Burungale, A. and Skinner, C.), Integers expressible as the sum of two rational cubes. Preprint, 2022. https://arxiv.org/abs/2210.10730 Google Scholar
Cai, L., Shu, J., and Tian, Y., Cube sum problem and an explicit Gross-Zagier formula . Amer. J. Math. 139(2017), no. 3, 785–816.CrossRefGoogle Scholar
Dasgupta, S. and Voight, J., Problem and mock Heegner points . Proc. Amer. Math. Soc. 146 (2018), no. 8, 3257–3273.CrossRefGoogle Scholar
Davis, M. and Putnam, H., Diophantine sets over polynomial rings. Illinois J. Math. 7(1963), 251–256.CrossRefGoogle Scholar
Davis, M., Putnam, H., and Robinson, J., The decision problem for exponential Diophantine equations . Ann. Math. 74(1961), no. 3, 425–436.Google Scholar
Denef, J. and Lipshitz, L., Diophantine sets over some rings of algebraic integers . J. London Math. Soc. 2(1978), no. 3, 385–391.Google Scholar
Garcia-Fritz, N. and Pasten, H., Towards Hilbert’s tenth problem for rings of integers through Iwasawa theory and Heegner points . Math. Ann. 377(2020), no. 3, 989–1013.Google Scholar
Hu, Y., Shu, J., and Yin, H., An explicit Gross–Zagier formula related to the Sylvester conjecture . Trans. Am. Math. Soc. 372(2019), no. 10, 6905–6925.Google Scholar
Jha, S., Majumdar, D., and Shingavekar, P., $3$ -Selmer group, ideal class groups and cube sum problem. Preprint, 2022. https://arxiv.org/abs/2207.12487 Google Scholar
Jha, S., Majumdar, D., and Sury, B., Binary cubic forms and rational cube sum problem. Preprint, 2023. https://arxiv.org/abs/2301.06970 Google Scholar
Koymans, P. and Pagano, C., Hilbert’s tenth problem via additive combinatorics. Preprint, 2024. https://arxiv.org/abs/2412.01768 Google Scholar
Kundu, D., Lei, A., and Sprung, F., Studying Hilbert’s 10th problem via explicit elliptic curves . Math. Ann. 390(2024), 5153–5183.Google Scholar
Majumdar, D. and Shingavekar, P., Cube sum problem for integers having exactly two distinct prime factors . Proc.-Math. Sci. 133(2023), no. 2, 22 Pages.Google Scholar
Matijasevic, Y., Enumerable sets are diophantine . Soviet Math. Dokl. 11(1970), 354–358.Google Scholar
Mazur, B. and Rubin, K., Ranks of twists of elliptic curves and Hilbert’s tenth problem . Invent. Math. 181(2010), no. 3, 541–575.Google Scholar
Perelli, A. and Pomykała, J., Averages of twisted elliptic $L$ -functions . Acta Arith. 80(1997), no. 2, 149–163.CrossRefGoogle Scholar
Poonen, B., Using elliptic curves of rank one towards the undecidability of Hilbert’s Tenth Problem over rings of algebraic integers . In: International algorithmic number theory symposium, 2002, pp. 33–42.CrossRefGoogle Scholar
Robinson, J., Unsolvable diophantine problems . Proc. Amer. Math. Soc. 22(1969), no. 2, 534–538.CrossRefGoogle Scholar
Shlapentokh, A., Elliptic curves retaining their rank in finite extensions and Hilbert’s tenth problem for rings of algebraic numbers . Trans. Amer. Math. Soc. 360(2008), no. 7, 3541–3555.CrossRefGoogle Scholar
Shnidman, A. and Weiss, A., Rank growth of elliptic curves over $n$ -th root extensions . Trans. Amer. Math. Soc. Ser. B 10 (2023), 482–506.Google Scholar
Sylvester, J., On certain ternary cubic-form equations . Amer. J. Math. 2(1879), no. 4, 357–393.Google Scholar