No CrossRef data available.
Published online by Cambridge University Press: 27 January 2025
Let  $\mathfrak{g}$ be the queer superalgebra
$\mathfrak{g}$ be the queer superalgebra 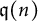 $\operatorname {\mathfrak{q}}(n)$ over the field of complex numbers
$\operatorname {\mathfrak{q}}(n)$ over the field of complex numbers 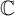 $\mathbb C$. For any associative, commutative, and finitely generated
$\mathbb C$. For any associative, commutative, and finitely generated 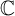 $\mathbb C$-algebra A with unity, we consider the loop Lie superalgebra
$\mathbb C$-algebra A with unity, we consider the loop Lie superalgebra 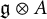 $\mathfrak{g} \otimes A$. We define a class of central operators for
$\mathfrak{g} \otimes A$. We define a class of central operators for 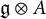 $\mathfrak{g} \otimes A$, which generalizes the classical Gelfand invariants. We show that they generate the algebra
$\mathfrak{g} \otimes A$, which generalizes the classical Gelfand invariants. We show that they generate the algebra 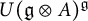 $U(\mathfrak{g} \otimes A)^{\mathfrak{g}}$. We also show that there are no non-trivial
$U(\mathfrak{g} \otimes A)^{\mathfrak{g}}$. We also show that there are no non-trivial 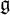 $\mathfrak{g}$-invariants of
$\mathfrak{g}$-invariants of  $U(\mathfrak{g} \otimes A)$ where
$U(\mathfrak{g} \otimes A)$ where 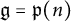 $\mathfrak{g}=\mathfrak{p}(n)$, the periplectic Lie superalgebra.
$\mathfrak{g}=\mathfrak{p}(n)$, the periplectic Lie superalgebra.