Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-24T18:46:46.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite group actions on dg categories and Hochschild homology

Part of: Homological algebra Homological methods

Published online by Cambridge University Press:  17 March 2025

Ville Nordström
Ville Nordström*
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR 97401, United States
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a finite group whose order is not divisible by the characteristic of the ground field 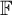$\mathbb {F}$. We prove a decomposition of the Hochschild homology groups of the equivariant dg category 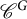$\mathscr {C}^G$ associated with the action of G on a small dg category 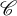$\mathscr {C}$ which admits finite direct sums. When, in addition, the ground field 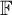$\mathbb {F}$ is algebraically closed this decomposition is related to a categorical action of 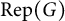$\text {Rep}(G)$ on 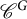$\mathscr {C}^G$ and the resulting action of the representation ring 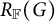$R_{\mathbb {F}}(G)$ on 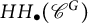$HH_\bullet (\mathscr {C}^G)$.

Keywords

Hochschild homologydg categoriesgroup actions

MSC classification

Primary: 16E40: (Co)homology of rings and algebras (e.g. Hochschild, cyclic, dihedral, etc.) 18G35: Chain complexes
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 21
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Belmans, P., Fu, L., and Krug, A., Hochschild cohomology of Hilbert schemes of points on surfaces. Preprint, 2023. arXiv:2309.06244 [math.AG]Google Scholar
Getzler, E. and Jones, J. D., The cyclic homology of crossed product algebras . J. Reine Angew. Math. 445(1993), 161–174.Google Scholar
Keller, B., On the cyclic homology of exact categories . J. Pure Appl. Algebra 136(1999), no. 1, 1–56.Google Scholar
Loday, J.-L., Cyclic homology. 2nd ed., Grundlehren der mathematischen Wissenschaften, Springer-Verlag, Berlin, 1998.Google Scholar
Mac Lane, S., Homology, Springer-Verlag, Berlin, 1975; 3rd corr. print.Google Scholar
Perry, A., Hochschild cohomology and group actions . Mathematische Zeitschrift 297(2021), no. 10, 1273–1292.Google Scholar
Polishchuk, A. and Positselski, L., Hochschild (co)homology of the second kind I . Trans. Amer. Math. Soc. 364(2012), no. 10, 5311–5368.Google Scholar
Quddus, S., Equivariant Cartan homotopy formulae for the crossed product of DG algebra . Rocky Mountain J. Math. 51(2021), no. 4, 1399–1406.Google Scholar