Hostname: page-component-6dbcb7884d-wnk8j Total loading time: 0 Render date: 2025-02-14T08:25:50.204Z Has data issue: false hasContentIssue false
  • English
  • Français

Fine Selmer groups of congruent p-adic Galois representations

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  29 September 2021

Sören Kleine Open the ORCID record for Sören Kleine [Opens in a new window]  and
Katharina Müller Open the ORCID record for Katharina Müller [Opens in a new window]
Sören Kleine*
Affiliation:
Institut für Theoretische Informatik, Mathematik und Operations Research, Universität der Bundeswehr München, Werner-Heisenberg-Weg 39, Neubiberg85577, Germany
Katharina Müller
Affiliation:
Mathematisches Institut, Georg-August-Universität Göttingen, Bunsenstraße 3-5, Göttingen 37073, Germany e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We compare the Pontryagin duals of fine Selmer groups of two congruent p-adic Galois representations over admissible pro-p, p-adic Lie extensions 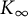$K_\infty $ of number fields K. We prove that in several natural settings the 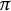$\pi $ -primary submodules of the Pontryagin duals are pseudo-isomorphic over the Iwasawa algebra; if the coranks of the fine Selmer groups are not equal, then we can still prove inequalities between the 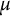$\mu $ -invariants. 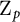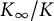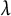In the special case of a $\mathbb {Z}_p$ -extension $K_\infty /K$ , we also compare the Iwasawa $\lambda $ -invariants of the fine Selmer groups, even in situations where the 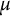$\mu $ -invariants are nonzero. Finally, we prove similar results for certain abelian non-p-extensions.

Keywords

Admissible p-adic Lie extensionabelian varietyp-adic Galois representationfine Selmer groupIwasawa invariants

MSC classification

Primary: 11R23: Iwasawa theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 3 , September 2022 , pp. 702 - 722
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmed, S. and Shekhar, S., $\lambda$ -invariants of Selmer groups of elliptic curves with positive $\mu$ -invariant . J. Ramanujan Math. Soc. 30(2015), no. 1, 115–133.Google Scholar
Barth, P., Iwasawa theory for one-parameter families of motives . Int. J. Number Theory 9(2013), no. 2, 257–319.10.1142/S1793042112501357CrossRefGoogle Scholar
Brink, D., Prime decomposition in the anti-cyclotomic extension . Math. Comp. 76(2007), no. 260, 2127–2138.CrossRefGoogle Scholar
Barman, R. and Saikia, A., A note on Iwasawa $\mu$ -invariants of elliptic curves . Bull. Braz. Math. Soc. (N.S.) 41(2010), no. 3, 399–407.10.1007/s00574-010-0018-8CrossRefGoogle Scholar
Coates, J., Fukaya, T., Kato, K., Sujatha, R., and Venjakob, O.. The $G{L}_2$ main conjecture for elliptic curves without complex multiplication . Publ. Math. Inst. Hautes Études Sci. 101(2005), 163–208.CrossRefGoogle Scholar
Coates, J. H. and Howson, S., Euler characteristics and elliptic curves. II . J. Math. Soc. Japan 53(2001), no. 1, 175–235.CrossRefGoogle Scholar
Coates, J. and Sujatha, R.. Fine Selmer groups of elliptic curves over $p$ -adic Lie extensions . Math. Ann. 331(2005), no. 4, 809–839.10.1007/s00208-004-0609-zCrossRefGoogle Scholar
Emerton, M., Pollack, R., and Weston, T.. Variation of Iwasawa invariants in Hida families . Invent. Math. 163(2006), no. 3, 523–580.10.1007/s00222-005-0467-7CrossRefGoogle Scholar
Greenberg, R., Iwasawa theory for $p$ -adic representations. In: Algebraic number theory, Adv. Stud. Pure Math., 17, Academic Press, Boston, MA, 1989, pp. 97–137.Google Scholar
Greenberg, R. and Vatsal, V., On the Iwasawa invariants of elliptic curves . Invent. Math. 142(2000), no. 1, 17–63.CrossRefGoogle Scholar
Goodearl, K. R. and Warfield, R. B. Jr., An introduction to noncommutative Noetherian rings , 2nd ed. London Mathematical Society Student Texts, 61, Cambridge University Press, Cambridge, 2004.Google Scholar
Hachimori, Y., Iwasawa $\lambda$ -invariants and congruence of Galois representations . J. Ramanujan Math. Soc. 26(2011), no. 2, 203–217.Google Scholar
Hatley, J., Rank parity for congruent supersingular elliptic curves . Proc. Amer. Math. Soc. 145(2017), no. 9, 3775–3786.CrossRefGoogle Scholar
Hatley, J. and Lei, A., Comparing anticyclotomic Selmer groups of positive coranks for congruent modular forms . Math. Res. Lett. 26(2019), no. 4, 1115–1144.CrossRefGoogle Scholar
Howson, S., Euler characteristics as invariants of Iwasawa modules . Proc. London Math. Soc. 85(2002), no. 3, 634–658.10.1112/S0024611502013680CrossRefGoogle Scholar
Imai, H., A remark on the rational points of Abelian varieties with values in cyclotomic ${\mathbb{Z}}_p$ -extensions . Proc. Japan Acad. 51(1975), 12–16.Google Scholar
Jha, S., Fine Selmer group of Hida deformations over non-commutative $p$ -adic Lie extensions . Asian J. Math. 16(2012), no. 2, 353–365.CrossRefGoogle Scholar
Katz, N. M. and Lang, S., Finiteness theorems in geometric classfield theory (with an appendix by K. A. Ribet). Enseign. Math. (2) 27(1981), 285–314, 315–319.Google Scholar
Kleine, S., Local behavior of Iwasawa’s invariants . Int. J. Number Theory 13(2017), no. 4, 1013–1036.CrossRefGoogle Scholar
Kundu, D., Growth of Selmer groups and fine Selmer groups in uniform pro- $p$ extensions . Ann. Math. Qué. 45(2021), no. 2, 347–362.10.1007/s40316-020-00147-1CrossRefGoogle Scholar
Lamplugh, J., An analogue of the Washington-Sinnott theorem for elliptic curves with complex multiplication I . J. Lond. Math. Soc. 91(2015), no. 3, 609–642.10.1112/jlms/jdv004CrossRefGoogle Scholar
Lang, S., Cyclotomic fields I and II , 2nd ed., Graduate Texts in Mathematics, 121, Springer-Verlag, New York, 1990. With an appendix by Karl Rubin.Google Scholar
Lang, S., Survey of diophantine geometry. Transl. from the Russian. Corr. 2nd printing, Springer, Berlin, 1997.Google Scholar
Lim, M. F., A remark on the $\mathcal{M}_H(G)$ -conjecture and Akashi series . Int. J. Number Theory 11(2015), no. 1, 269–297.CrossRefGoogle Scholar
Lim, M. F., Comparing the $\pi$ -primary submodules of the dual Selmer groups . Asian J. Math. 21(2017), no. 6, 1153–1181.CrossRefGoogle Scholar
Lim, M. F., Notes on the fine Selmer groups . Asian J. Math. 21(2017), no. 2, 337–361.10.4310/AJM.2017.v21.n2.a5CrossRefGoogle Scholar
Lim, M. F. and Kumar Murty, V., The growth of fine Selmer groups . J. Ramanujan Math. Soc. 31(2016), no. 1, 79–94.Google Scholar
Lim, M. F. and Sujatha, R., Fine Selmer groups of congruent Galois representations . J. Number Theory 187(2018), 66–91.10.1016/j.jnt.2017.10.018CrossRefGoogle Scholar
Mattuck, A., Abelian varieties over $p$ -adic ground fields . Ann. Math. 62(1955), no. 2, 92–119.CrossRefGoogle Scholar
Mazur, B. and Rubin, K., Kolyvagin systems . Mem. Amer. Math. Soc. 168(2004), no. 799, viii+96.Google Scholar
Neukirch, J., Schmidt, A., and Wingberg, K.. Cohomology of number fields, 2nd ed., Springer, Berlin, 2008.10.1007/978-3-540-37889-1CrossRefGoogle Scholar
Ponsinet, G., On the structure of signed Selmer groups . Math. Z. 294(2020), no. 3–4, 1635–1658.10.1007/s00209-019-02328-3CrossRefGoogle Scholar
Sharma, A. C., Iwasawa invariants for the false-Tate extension and congruences between modular forms . J. Number Theory 129(2009), no. 8, 1893–1911.10.1016/j.jnt.2009.03.001CrossRefGoogle Scholar
Sujatha, R. and Witte, M., Fine Selmer groups and isogeny invariance. In: Geometry, algebra, number theory, and their information technology applications, Springer Proc. Math. Stat., 251, Springer, Cham, 2018, pp. 419–444.10.1007/978-3-319-97379-1_19CrossRefGoogle Scholar
Venjakob, O., On the structure theory of the Iwasawa algebra of a $p$ -adic Lie group . J. Eur. Math. Soc. 4(2002), 271–311.CrossRefGoogle Scholar