Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-24T22:42:30.171Z Has data issue: false hasContentIssue false
  • English
  • Français

Families of Young functions and limits of Orlicz norms

Part of: Classical measure theory Linear function spaces and their duals

Published online by Cambridge University Press:  29 May 2023

Sullivan F. MacDonald  and
Scott Rodney
Sullivan F. MacDonald
Affiliation:
Department of Mathematics & Statistics, McMaster University, Hamilton, ON L8S4L8, Canada e-mail: [email protected]
Scott Rodney*
Affiliation:
Department of Mathematics, Physics and Geology, Cape Breton University, Sydney, NS B1Y3V3, Canada
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a $\sigma $-finite measure space 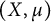$(X,\mu )$, a Young function 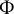$\Phi $, and a one-parameter family of Young functions 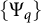$\{\Psi _q\}$, we find necessary and sufficient conditions for the associated Orlicz norms of any function 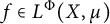$f\in L^\Phi (X,\mu )$ to satisfy

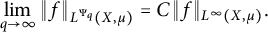$$\begin{align*}\lim_{q\rightarrow \infty}\|f\|_{L^{\Psi_q}(X,\mu)}=C\|f\|_{L^\infty(X,\mu)}. \end{align*}$$

The constant C is independent of f and depends only on the family 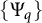$\{\Psi _q\}$. Several examples of one-parameter families of Young functions satisfying our conditions are given, along with counterexamples when our conditions fail.

Keywords

Orlicz spacesfunctional analysisclassical analysis

MSC classification

Primary: 28A25: Integration with respect to measures and other set functions 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 1 , March 2024 , pp. 26 - 39
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

S. Rodney was supported by the NSERC Discovery Grant Program. S.F. MacDonald was supported by the NSERC USRA Program and the Department of Mathematics & Statistics at McMaster University.

References

Cruz-Uribe, D. and Rodney, S., Bounded weak solutions to elliptic PDE with data in Orlicz spaces . J. Differential Equations 297(2021), 409–432.CrossRefGoogle Scholar
Cruz-Uribe, D. and Rodney, S., A note on the limit of Orlicz norms . Real Anal. Exchange 48(2023), 77–82.Google Scholar
Mailhot, A., On the limit of Orlicz norms. Undergraduate thesis, Cape Breton University, 2022. http://faculty.cbu.ca/srodney/pdf/theses/thesisam.pdf.Google Scholar
Rao, M. N. and Ren, Z. D., Theory of Orlicz spaces, Marcel-Dekker, New York, 1991.Google Scholar
Royden, H. L., Real analysis, third edition, MacMillan, New York, 1988.Google Scholar
Rudin, W., Real and complex analysis, third edition, McGraw Hill, New York, 1987.Google Scholar
Trudinger, N. S. and Donaldson, T. K., Orlicz–Sobolev spaces and imbedding theorems . J. Funct. Anal. 8(1971), 52–75.Google Scholar