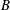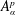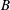Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Baranov, Anton Dmitrievich
and
Kayumov, Ilgiz Rifatovich
2022.
Оценки интегралов от производных рациональных функций в многосвязных областях на плоскости.
Известия Российской академии наук. Серия математическая,
Vol. 86,
Issue. 5,
p.
5.
Baranov, Anton Dmitrievich
and
Kayumov, Ilgiz Rifatovich
2022.
Estimates for the
integrals of derivatives of rational functions in multiply connected
domains in the plane.
Izvestiya: Mathematics,
Vol. 86,
Issue. 5,
p.
839.