Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-20T00:06:47.303Z Has data issue: false hasContentIssue false
  • English
  • Français

Concordance, Crossing Changes, and Knots in Homology Spheres

Part of: Low-dimensional topology

Published online by Cambridge University Press:  16 December 2019

Christopher W. Davis
Christopher W. Davis*
Affiliation:
Department of Mathematics, University of Wisconsin–Eau Claire, USA Email: [email protected] URL: www.uwec.edu/daviscw
Get access Rights & Permissions [Opens in a new window]

Abstract

Any knot in 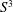$S^{3}$ can be reduced to a slice knot by crossing changes. Indeed, this slice knot can be taken to be the unknot. In this paper we study the question of when the same holds for knots in homology spheres. We show that a knot in a homology sphere is nullhomotopic in a smooth homology ball if and only if that knot is smoothly concordant to a knot that is homotopic to a smoothly slice knot. As a consequence, we prove that the equivalence relation on knots in homology spheres given by cobounding immersed annuli in a homology cobordism is generated by concordance in homology cobordisms together with homotopy in a homology sphere.

MSC classification

Primary: 57M25: Knots and links in $S^3$
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 4 , December 2020 , pp. 744 - 754
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Austin, D. and Rolfsen, D., Homotopy of knots and the Alexander polynomial. Canad. Math. Bull. 42(1999), 257–262. https://doi.org/10.4153/CMB-1999-031-6CrossRefGoogle Scholar
Casson, A. and Freedman, M., Atomic surgery problems. In: Four-manifold theory (Durham, N.H., 1982). Contemp. Math., 35, Amer. Math. Soc., Providence, RI, 1984, pp. 181–199. https://doi.org/10.1090/conm/035/780579CrossRefGoogle Scholar
Daemi, A., Chern–Simons functional and the homology cobordism group. 2018. arxiv:1810.08176Google Scholar
Davis, C. W., Topological concordance of knots in homology spheres and the solvable filtration. J. Topology 13(2019), 343–355.CrossRefGoogle Scholar
Davis, C. W. and Ray, A., Satellite operators as group actions on knot concordance. Algebr. Geom. Topol. 16(2016), 945–969. https://doi.org/10.2140/agt.2016.16.945CrossRefGoogle Scholar
Davis, J. F. and Kirk, P., Lecture notes in algebraic topology. Graduate Studies in Mathematics, 35, American Mathematical Society, Providence, RI, 2001. https://doi.org/10.1090/gsm/035CrossRefGoogle Scholar
Fox, R. H. and Milnor, J. W., Singularities of 2-spheres in 4-space and equivalence of knots. (Abstract) Bulletin of Amer. Math. Soc. 63(1957), 406.Google Scholar
Fox, R. H. and Milnor, J. W., Singularities of 2-spheres in 4-space and cobordism of knots. Osaka J. Math. 3(1966), 257–267.Google Scholar
Freedman, M. H. and Quinn, F., Topology of 4-manifolds. Princeton Mathematical Series, 39, Princeton University Press, Princeton, NJ, 1990.Google Scholar
Gompf, R. E. and Stipsicz, A. I., 4-manifolds and Kirby calculus. Graduate Studies in Mathematics, 20, American Mathematical Society, Providence, RI, 1999. https://doi.org/10.1090/gsm/020CrossRefGoogle Scholar
Hom, J., Levine, A. S., and Lidman, T., Knot concordance in homology cobordisms. 2018. arxiv:1801.07770Google Scholar
Kojima, S., Piecewise linear Dehn’s lemma in 4 dimensions. Proc. Japan Acad. Ser. A Math. Sci. 55(1979), 65–67.CrossRefGoogle Scholar
Levine, A. S., Nonsurjective satellite operators and piecewise-linear concordance. Forum Math. Sigma 4(2016), e34. https://doi.org/10.1017/fms.2016.31CrossRefGoogle Scholar
Owens, B. and Strle, S., Immersed disks, slicing numbers and concordance unknotting numbers. Comm. Anal. Geom. 24(2016), 1107–1138. https://doi.org/10.4310/CAG.2016.v24.n5.a8CrossRefGoogle Scholar