Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T15:47:54.520Z Has data issue: false hasContentIssue false
  • English
  • Français

A Common Extension of Arhangel’skĭ’s Theorem and the Hajnal–Juhász Inequality

Part of: Fairly general properties Generalities

Published online by Cambridge University Press:  06 January 2020

Angelo Bella  and
Santi Spadaro
Angelo Bella
Affiliation:
Dipartimento di Matematica e Informatica, viale A. Doria 6, 95125Catania, Italy Email: [email protected]@gmail.com
Santi Spadaro
Affiliation:
Dipartimento di Matematica e Informatica, viale A. Doria 6, 95125Catania, Italy Email: [email protected]@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a result about 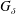$G_{\unicode[STIX]{x1D6FF}}$ covers of a Hausdorff space that implies various known cardinal inequalities, including the following two fundamental results in the theory of cardinal invariants in topology: 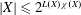$|X|\leqslant 2^{L(X)\unicode[STIX]{x1D712}(X)}$ (Arhangel’skiĭ) and 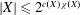$|X|\leqslant 2^{c(X)\unicode[STIX]{x1D712}(X)}$ (Hajnal–Juhász). This solves a question that goes back to Bell, Ginsburg and Woods’s 1978 paper (M. Bell, J.N. Ginsburg and R.G. Woods, Cardinal inequalities for topological spaces involving the weak Lindelöf number, Pacific J. Math. 79(1978), 37–45) and is mentioned in Hodel’s survey on Arhangel’skiĭ’s Theorem (R. Hodel, Arhangel’skii’s solution to Alexandroff’s problem: A survey, Topology Appl. 153(2006), 2199–2217).

In contrast to previous attempts, we do not need any separation axiom beyond 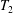$T_{2}$.

Keywords

cardinality boundcardinal invariantcellularityLindelöfweakly Lindelöfpiecewise weakly Lindelöf

MSC classification

Primary: 54A25: Cardinality properties (cardinal functions and inequalities, discrete subsets)
Secondary: 54D20: Noncompact covering properties (paracompact, Lindelöf, etc.) 54D10: Lower separation axioms ($T_0$--$T_3$, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 1 , March 2020 , pp. 197 - 203
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research that led to the present paper was partially supported by a grant of the group GNSAGA of INdAM.

References

Alas, O. T., More topological cardinal inequalities. Colloq. Math. 65(1993), 165–168.CrossRefGoogle Scholar
Arhangel’skiĭ, A. V., The power of bicompacta with first axiom of countability. Soviet Math. Dokl. 10(1969), 951–955.Google Scholar
Arhangel’skiĭ, A. V., A theorem about cardinality. Russian Math. Surveys 34(1979), 153–154.CrossRefGoogle Scholar
Arhangel’skiĭ, A. V., A generic theorem in the theory of cardinal invariants of topological spaces. Comment. Math. Univ. Carolin. 36(1995), 303–325.Google Scholar
Bell, M., Ginsburg, J. N., and Woods, R. G., Cardinal inequalities for topological spaces involving the weak Lindelöf number. Pacific J. Math. 79(1978), 37–45.CrossRefGoogle Scholar
Bella, A. and Cammaroto, F., On the cardinality of Urysohn spaces. Canad. Math. Bull. 31(1988), 153–158.CrossRefGoogle Scholar
Bella, A. and Carlson, N., On cardinality bounds involving the weak Lindelöf degree. Quaest. Math. 41(2018), 99–113.CrossRefGoogle Scholar
Bella, A. and Spadaro, S., Cardinal invariants for the G 𝛿-topology. Colloq. Math. 156(2019), 123–133.CrossRefGoogle Scholar
Bella, A. and Spadaro, S., Infinite games and cardinal properties of topological spaces. Houston J. Math. 41(2015), 1063–1077.Google Scholar
Dow, A., An introduction to applications of elementary submodels to topology. Topology Proc. 13(1988), 17–72.Google Scholar
Engelking, R., General topology. Heldermann–Verlag, 1989.Google Scholar
Gotchev, I., Cardinalities of weakly Lindelöf spaces with regular G 𝜅 diagonals. Topology Appl. 259(2019), 80–89.CrossRefGoogle Scholar
Hajnal, A. and Juhász, I., Discrete subspaces of topological spaces. Indag. Math. 29(1967), 343–356.CrossRefGoogle Scholar
Hodel, R. E., Cardinal Functions I. In: Handbook of set-theoretic topology, eds. K. Kunen and J. E. Vaughan, North Holland, Amsterdam, 1984, pp. 1–61.CrossRefGoogle Scholar
Hodel, R. E., Arhangel’skĭ’s solution to Alexandroff’s problem: A survey. Topology Appl. 153(2006), 2199–2217.CrossRefGoogle Scholar