Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-25T02:44:47.965Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundedness on Triebel–Lizorkin spaces for the Calderón commutator with rough kernel

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  12 March 2025

Rong Liang  and
Xiangxing Tao Open the ORCID record for Xiangxing Tao [Opens in a new window]
Rong Liang
Affiliation:
Department of Mathematics, School of Science, Zhejiang University of Science and Technology, Hangzhou 310023, People’s Republic of China e-mail: [email protected]
Xiangxing Tao*
Affiliation:
Department of Mathematics, School of Science, Zhejiang University of Science and Technology, Hangzhou 310023, People’s Republic of China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, the authors consider the boundedness on Triebel–Lizorkin spaces for the d-dimensional Calderón commutator defined by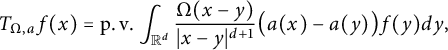

$$ \begin{align*}T_{\Omega,a}f(x)=\mathrm{p.\,v.}\int_{\mathbb{R}^d}\frac{\Omega(x-y)}{|x-y|^{d+1}}\big(a(x)-a(y)\big)f(y){d}y,\end{align*} $$
where $\Omega $ is homogeneous of degree zero, integrable on 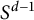$S^{d-1}$ and has a vanishing moment of order one, a is a Lipschitz function on 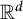$\mathbb {R}^d$. The authors proved that if
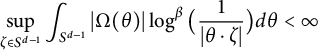$$ \begin{align*}\sup_{\zeta\in S^{d-1}}\int_{S^{d-1}}|\Omega(\theta)|\log ^{\beta} \big(\frac{1}{|\theta\cdot\zeta|}\big)d\theta<\infty\end{align*} $$
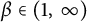with $\beta \in (1,\,\infty )$, then 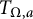$T_{\Omega ,a}$ is bounded on Triebel–Lizorkin spaces 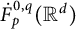$\dot {F}_{p}^{0,q}(\mathbb {R}^d)$ for 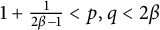$1+\frac {1}{2\beta -1}<p,q<2\beta $.

Keywords

Calderón commutatorTriebel–Lizorkin spaceLittlewood–Paley theoryCalderón reproducing formula

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 13
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The research was supported by the NNSF of China under grants #12271483, #11971295, and #11771399.

References

Al-Qassem, H. M., Cheng, L. C., and Pan, Y., Boundedness of rough integral operators on Triebel-Lizorkin spaces . Publ. Mat. 5(2012), 261–277.Google Scholar
Calderón, A. P., Commutators of singular integral operators . Proc. Nat. Acad. Sci. U.S.A. 53(1965), 1092–1099.Google Scholar
Calderón, A. P., Commutators, singular integrals on Lipschitz curves and application . In: Proceedings of the international congress of mathematicians , Helsinki, 1978, pp. 86–95.Google Scholar
Chen, J., Fan, D., and Ying, Y., Singular integral operators on function spaces . J. Math. Anal. Appl. 276(2002), 691–708.Google Scholar
Chen, J., Hu, G., and Tao, X., ${L}^p({\mathbb{R}}^d)$ boundedness for the Calderón commutator with rough kernel . J. Geom. Anal. 33(2023), Article 14. https://doi.org/10.1007/s12220-022-01056-1.Google Scholar
Chen, J., Hu, G., and Tao, X., ${L}^p({\mathbb{R}}^d)$ boundedness for a class of nonstandard singular integral operators . J. Fourier Anal. Appl. 30(2024), Article 50. https://doi.org/10.1007/s00041-024-10104-z.Google Scholar
Chen, J. and Zhang, C., Boundedness of rough singular integral operators on the Triebel-Lizorkin spaces . J. Math. Anal. Appl. 337(2008), 1048–1052.Google Scholar
Ding, Y. and Lai, X., Weak type $\left(1,1\right)$ bounded criterion for singular integral with rough kernel and its applications. Trans. Amer. Math. Soc. 371(2019), 1649–1675.Google Scholar
Duoandikoetxea, J., Extrapolation of weights revisited: New proofs and sharp bounds . J. Funct. Anal. 260(2011), 1886–1901.Google Scholar
Fan, D. and Zhao, F., Littlewood-Paley functions and Triebel-Lizorkin spaces, and Besov spaces . Appl. Theory Appl. 37(2021), 267–288.Google Scholar
Fefferman, C. and Stein, E. M., Some maximal inequalities . Amer. J. Math. 93(1971), 107–115.Google Scholar
Grafakos, L., Modern fourier analysis. 2nd ed., GTM, 250, Springer, New York, NY, 2008.Google Scholar
Grafakos, L. and Stefanov, A., ${L}^p$ bounds for singular integrals and maximal singular integrals with rough kernels . Indiana Univ. Math. J. 47(1998), 455–469.Google Scholar
Hofmann, S., Weighted norm inequalities for commutators of rough singular integrals . Indiana Univ. Math. J. 39(1990), 1275–1304.Google Scholar
Hu, G. and Liu, J., Boundedness of the Calderón commutator with a rough kernel on Triebel-Lizorkin spaces . Acta Math. Sci. 43B(2023), 1618–1632.Google Scholar
Hu, G., Tao, X., Wang, Z., and Xue, Q., On the boundedness of nonstandard singular integral operators . J. Fourier Anal. Appl. 30(2024), Article 32. https://doi.org/10.1007/s00041-024-10086-y.Google Scholar
Pan, Y., Wu, Q., and Yang, D., A remark on multilinear singular integrals with rough kernels . J. Math. Anal. Appl. 253(2001), 310–321.Google Scholar
Tao, X. and Hu, G., An estimate for the composition of rough singular integral operators . Can. Math. Bull. 64(2021), no. 4, 911–922.Google Scholar
Tao, X. and Hu, G., A bilinear sparse domination for the maximal singular integral operators with rough kernels . J. Geom. Anal. 34(2024), Article 162. https://doi.org/10.1007/s12220-024-01607-8.Google Scholar