For functions in 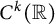$C^k(\mathbb {R})$ which commute with a translation, we prove a theorem on approximation by entire functions which commute with the same translation, with a requirement that the values of the entire function and its derivatives on a specified countable set belong to specified dense sets. 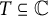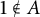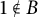Using this theorem, we show that if A and B are countable dense subsets of the unit circle $T\subseteq \mathbb {C}$ with $1\notin A$ , $1\notin B$ , then there is an analytic function 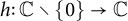$h\colon \mathbb {C}\setminus \{0\}\to \mathbb {C}$ that restricts to an order isomorphism of the arc 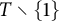$T\setminus \{1\}$ onto itself and satisfies 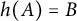$h(A)=B$ and 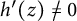$h'(z)\not =0$ when 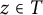$z\in T$ . This answers a question of P. M. Gauthier.