Article contents
An energy decomposition theorem for matrices and related questions
Published online by Cambridge University Press: 15 May 2023
Abstract
Given 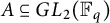 $A\subseteq GL_2(\mathbb {F}_q)$, we prove that there exist disjoint subsets
$A\subseteq GL_2(\mathbb {F}_q)$, we prove that there exist disjoint subsets 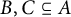 $B, C\subseteq A$ such that
$B, C\subseteq A$ such that 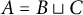 $A = B \sqcup C$ and their additive and multiplicative energies satisfying
$A = B \sqcup C$ and their additive and multiplicative energies satisfying 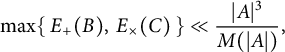 $$\begin{align*}\max\{\,E_{+}(B),\, E_{\times}(C)\,\}\ll \frac{|A|^3}{M(|A|)}, \end{align*}$$
$$\begin{align*}\max\{\,E_{+}(B),\, E_{\times}(C)\,\}\ll \frac{|A|^3}{M(|A|)}, \end{align*}$$
where 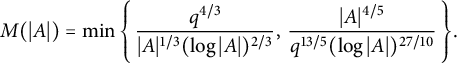 $$ \begin{align*} M(|A|) = \min\Bigg\{\,\frac{q^{4/3}}{|A|^{1/3}(\log|A|)^{2/3}},\, \frac{|A|^{4/5}}{q^{13/5}(\log|A|)^{27/10}}\,\Bigg\}. \end{align*} $$
$$ \begin{align*} M(|A|) = \min\Bigg\{\,\frac{q^{4/3}}{|A|^{1/3}(\log|A|)^{2/3}},\, \frac{|A|^{4/5}}{q^{13/5}(\log|A|)^{27/10}}\,\Bigg\}. \end{align*} $$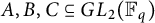 $A, B, C\subseteq GL_2(\mathbb {F}_q)$, we have
$A, B, C\subseteq GL_2(\mathbb {F}_q)$, we have 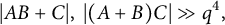 $$\begin{align*}|AB+C|, ~|(A+B)C|\gg q^4,\end{align*}$$
$$\begin{align*}|AB+C|, ~|(A+B)C|\gg q^4,\end{align*}$$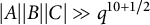 $|A||B||C|\gg q^{10 + 1/2}$. These improve earlier results due to Karabulut, Koh, Pham, Shen, and Vinh ([2019], Expanding phenomena over matrix rings,
$|A||B||C|\gg q^{10 + 1/2}$. These improve earlier results due to Karabulut, Koh, Pham, Shen, and Vinh ([2019], Expanding phenomena over matrix rings, 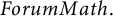 $Forum Math.$, 31, 951–970).
$Forum Math.$, 31, 951–970).
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
References
- 1
- Cited by



